Summing Sequences

Let n be the number of integers in the list. Then for any particular integer k, calculating N(k) can be done in O(n log n) time.

Consider the list [3,4,-6,7,-8,9]. To aid in evaluating sums of contiguous subsequences, we can calculate the running sum from the leftmost number: for the given list, we get

[0, 0+3=3,3+4=7,7+(-6)=1,1+7=8,8+(-8)=0,0+9=9]

where the leftmost zero is used to represent the 'sum' of an empty sequence. Call this sequence ${S_0,S_1,...,S_n}$ To calculate $N(k)$ , we can inspect for pairs of integers $S_i,S_j$ such that $i<j$ and $S_j-S_i = k$

A naive $O(n^2)$ proceeds by trying all $_{n+1}C_2$ pairs $(S_i,S_j)$ with $i<j$ and checking if their difference is $k$ .

An improvement to the above solution proceeds by inspecting each $S_i$ for $i=1,...,n$ and counting how many integers $S_j$ there are with $j<i$ and $S_j = S_i - k$ . Counting all $S_j's$ can be done in O(log n) time by inserting the elements of the runnning-sum sequence in a red-black tree.

Here is my code in C++ implementing the above solution:

#include< iostream>
#include< cstdio>
#include< map>
using namespace std;

int main(){
   map<int,int> H;
   H[0]=1;
   int n;
   int curr=0;
   int a[]={11,2,9,14};
   int ans=0;
   while(true){
      if (scanf("%d",&n)==-1) break;
      curr+=n;
      for(int i=0; i<4; i++){
         int target=curr-a[i];
         map<int,int>::iterator it=H.find(target);
         if (it!=H.end()) ans+=it->second;
      }
      if (H.find(curr)==H.end()) H[curr]=1;
      else H[curr]++;
   }
   cout<<ans<<endl;
}

My O( $n^2$ ) solution in Ruby is

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

a = %w(4 2 10 3 -9 10 1 8 -1 -10 -9 -4 6 -1 10 -6 -5 9 5 -2 6 3 6 0 6 8 -2 -4 8 -3 9 5 -2 4 6 10 -5 3 4 -5 0 4 -4 10 -3 7 -8 -2 -4 2 10 7 -10 10 -1 -9 -8 4 10 -10 -8 -6 9 8 -5 6 -9 -10 -10 -5 2 -4 -5 -1 -9 -1 -3 -3 -9 9 5 8 -8 -3 4 7 -9 2 4 -6 3 10 -3 3 0 4 4 -7 9 8 6 2 3 4 1 3 10 -9 8 6 10 -3 2 2 5 5 -7 2 -8 0 -3 7 -6 10 3 3 4 -8 -8 -5 -7 -8 -9 5 8 4 -7 -3 -5 -3 7 -9 4 4 4 -6 4 10 0 -1 5 -1 -9 -8 2 5 4 6 -4 7 3 7 -2 10 7 8 -4 6 -7 3 -4 2 -9 0 6 9 2 6 7 1 10 7 9 5 4 -4 2 -9 5 -2 -7 3 -6 10 -2 3 -3 -10 6 4 2 -5 -2 -9 -5 -10 -7 0 6 7 6 7 -4 -10 -9 2 4 -9 4 0 5 -5 9 10 5 6 -10 4 -5 -5 2 -1 8 -7 6 9 -3 5 1 4 -1 -10 -2 -4 -8 1 0 1 -8 -6 1 1 -4 7 -5 -7 -3 -10 4 2 1 -6 8 10 -10 0 -10 -3 -10 7 -8 4 5 -5 10 -3 -3 7 -4 -7 -3 5 7 1 -8 2 7 1 10 8 -3 9 9 -9 7 -2 -6 10 -4 -6).map{|l|l.to_i}

def mCS(a)
    h = Hash.new{0}
    a.length.times{|i0|
        raise if a[i0].nil? # paranoia is a virtue
        s = 0
        (i0..a.length-1).each{|i1|
            raise if a[i1].nil? # paranoia is a virtue again
            s += a[i1]
            h[s] += 1
        }
    }
    h
end

h = mCS([1,1,1])

raise unless h.inspect == '{1=>3, 2=>2, 3=>1}' # smoke test

h = mCS(a)

s = h[11] + h[2] + h[9] + h[14]
p s.commify # code not defined here turns 1113 into '1,113'
# correct 113

Python 3.5.1:

#Summing Sequences
file = open("alist.txt", "r")
def N(alist,s):
    count=0
    for index1 in range(len(alist)):
        for index2 in range(index1,len(alist)):
            asum = sum(alist[i] for i in range(index1,index2+1))
            if asum==s:
            count+=1
    return count

biglist = [int(line.strip()) for line in file]
print(N(biglist,11) + N(biglist,2) + N(biglist,9) + N(biglist,14))

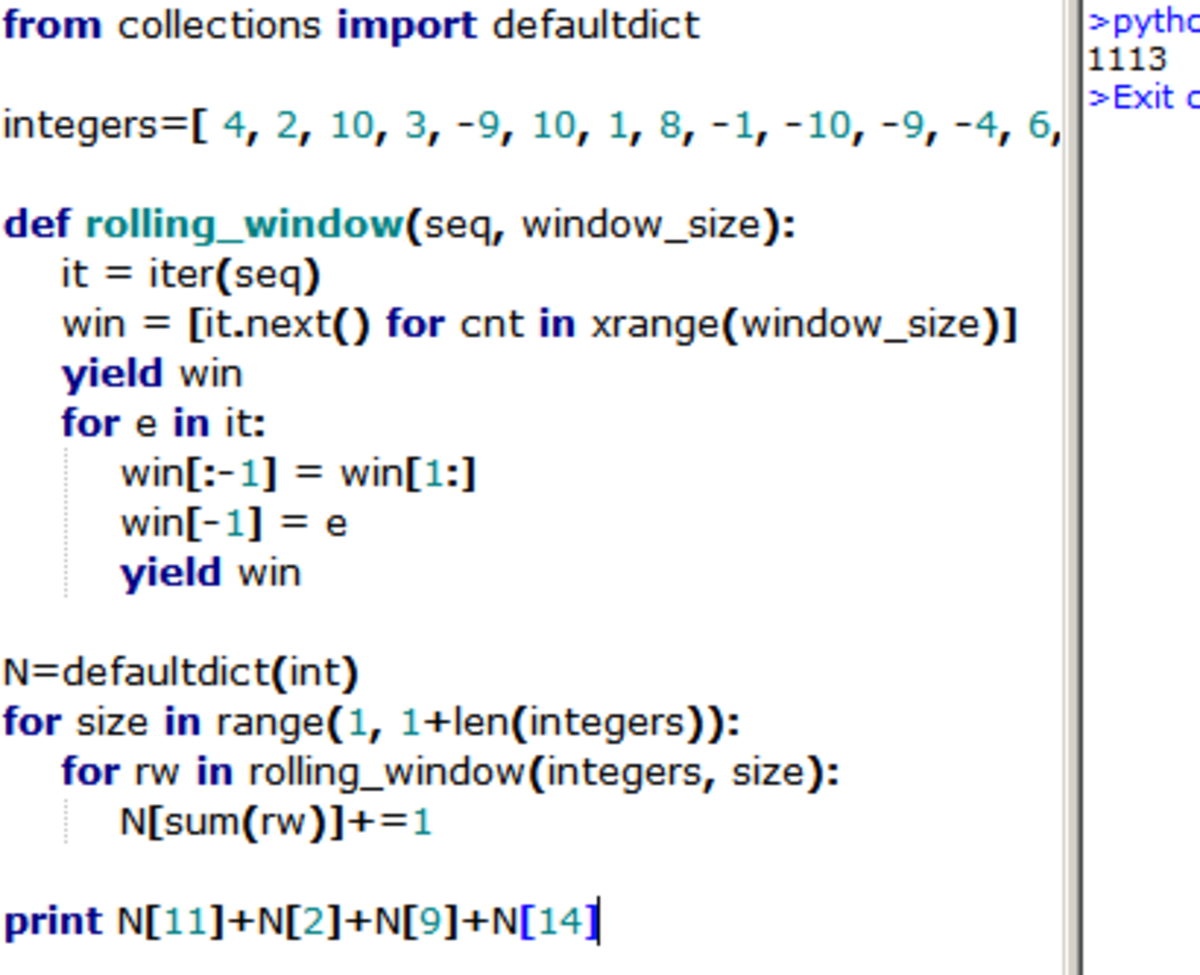
This is another rolling/sliding window problem.

Solution in Python; will run 'len(list)' iterations over the list, taking into account larger subsets that sum up to the number (remember that 'sublists_sum(1,[-1,1,1]) == 3' because the contiguous subsequence {-1,1,1} sums up to 1).

def sublists_sum(number,list_of_numbers):
      sequences = 0
      list_len = len(list_of_numbers)
      for i in range(0,list_len):
              total_sum = 0
              for z in range(i,list_len):
                      total_sum += list_of_numbers[z]
                      if (total_sum == number):
                              sequences += 1
      return sequences

Solution in AutoHotkey

global file := A_Desktop "\nlist.txt"   ; THE FILE WITH THE LIST
msgbox % N(11) + N(2) + N(9) + N(14)
return

N(N){
    o := {}
    loop, read, % file
        o.Insert(A_LoopReadLine)
    tl := o.MaxIndex() , ans := 0
    loop % tl 
    {
        i := A_index , s := 0
        loop % tl-i+1
        {
            s += o[i+A_index-1]
            if (s==N)
                ans++
        }
    }
    return ans
}

We use the following Python 2 code to make a generator for all the subsequences of a list:

def subsequences(li):
    for length in xrange(1, len(li) + 1):
        for start in xrange(0, len(li) - length + 1):
            yield li[start : start + length]

Then, we can store the data to a list and finish the problem with:

import urllib2
ans = 0
data = map(int, urllib2.urlopen('https://gist.githubusercontent.com/brilliant-problems/e154b00845f6c922a4b7/raw/cec07a3ae48c7b6964b16ef82e37b4268367e240/cs_subsequence_sums').read().split())
for i in subsequences(data):
    if (sum(i) == 9) or (sum(i) == 11) or (sum(i) == 2) or (sum(i) == 14):
        ans += 1
print ans

Our final code is: http://pastebin.com/9ZNZwN33