Summing up

Algebra Level 2

If $n=1983!$ then compute the sum $\displaystyle{ \frac{1}{\log_{2} {n}}+\frac{1}{\log_{3} {n}}+\frac{1}{\log_{4} {n}} + \ldots+\frac{1}{\log_{1983} {n}} }$

The answer is 1.

3 solutions

Datu Oen
Mar 20, 2014

Note that $\log_a{b} = \frac{\log{b}}{\log{a}}$

Then

$\frac{1}{\log_2{n}} = \frac{\log 2}{\log n}$ ,

$\frac{1}{\log_3{n}} = \frac{\log 3}{\log n}$ ... $\frac{1}{\log_{1983}{n}} = \frac{\log 1983}{\log n}$

$\frac{1}{\log_2{n}} + \frac{1}{\log_3{n}} +...+\frac{1}{\log_{1983}{n}} = \frac{\log 2}{\log n} + \frac{\log 3}{\log n} + \frac{\log 1983}{\log n}$

$\frac{\log 2}{\log n} + \frac{\log 3}{\log n} + \frac{\log 1983}{\log n} = \frac{\log 2 + \log 3 + ... + log 1983}{\log n} = \frac{\log 1983!}{\log n}$

Since $n = 1983!$ , then $\frac{\log 1983!}{\log n} = 1$

Datu Oen could you tell me what is the name of the subject that you use on this kind of sum? thanks.

Gustavo Oliveira - 7 years, 2 months ago

Logarithms and it's applications. You also need to learn indices & exponents to understand them.

A Brilliant Member - 7 years ago

how log2+log3+.............+log1983=log1983! explain please

muhmd sani - 7 years ago

$log(2)+log(3)+....+log(1983)$ can be written as:

$log(2\times3\times....\times1983)$ (since $log_{a}(b)+log_{a}(c)=log_{a}(bc)$ - Law of Logarithm)

$1983!=1\times2\times3\times....\times1983=2\times3\times....\times1983$

So, $log(2\times3\times....\times1983)=log(1983!)$

Therefore, $\boxed{log(2)+log(3)+....+log(1983) =log(1983!)}$

Saurabh Mallik - 6 years, 9 months ago

Abhisek Mohanty
Mar 29, 2015

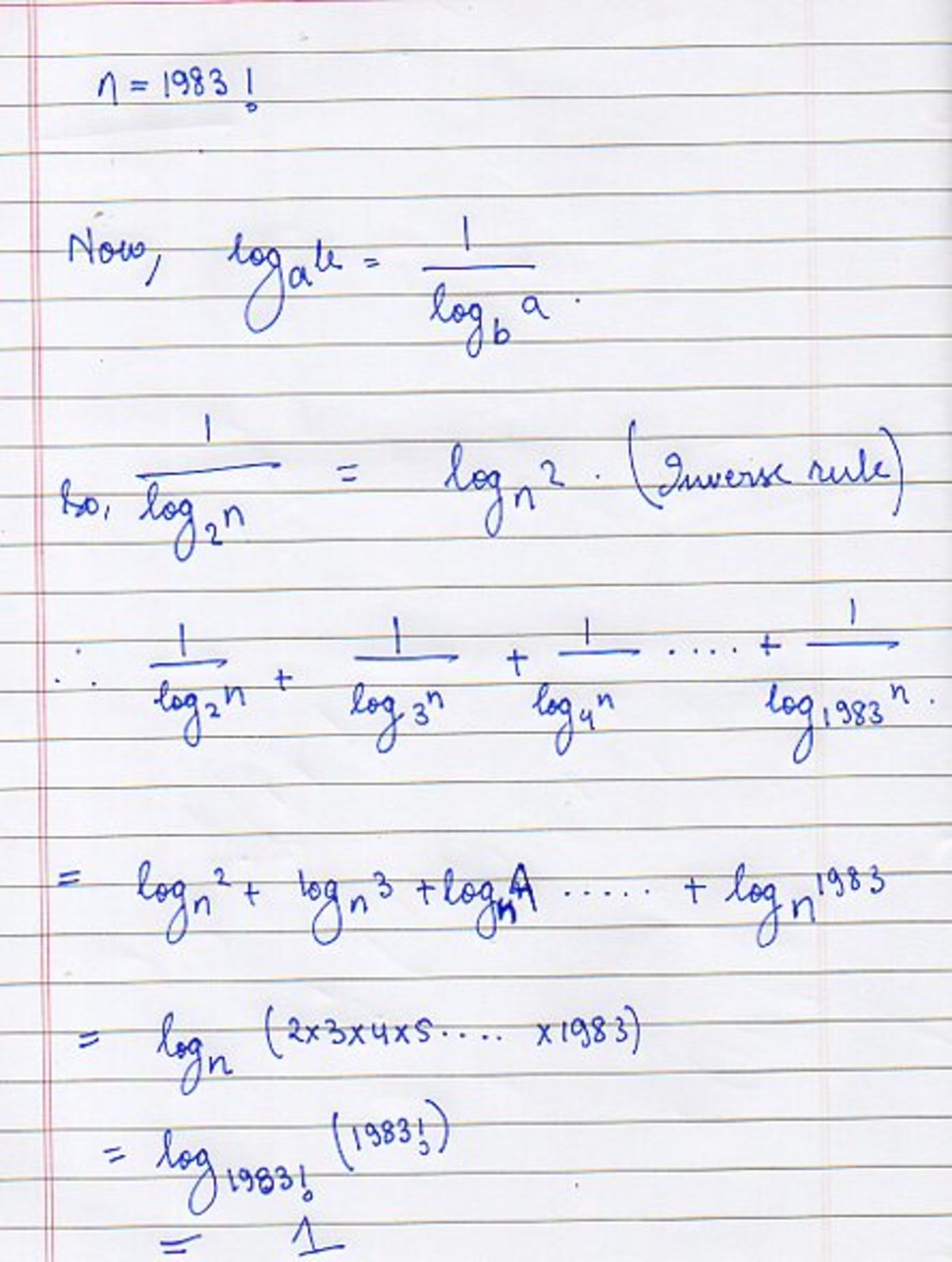What about this !!!!!!!!!!!!!!!

Bernardo Sulzbach
Jun 19, 2014

The problem statement is wrong. There are 2 logs with base 3.

Thanks. I have updated the question accordingly.

For problems with errors, you will get a much faster response if you report the problem, by selecting "report" from the "dot dot dot" menu in the lower right corner.

Calvin Lin Staff - 6 years, 11 months ago

Summing up

The answer is 1.

3 solutions

0 pending reports