Sun & Beaches
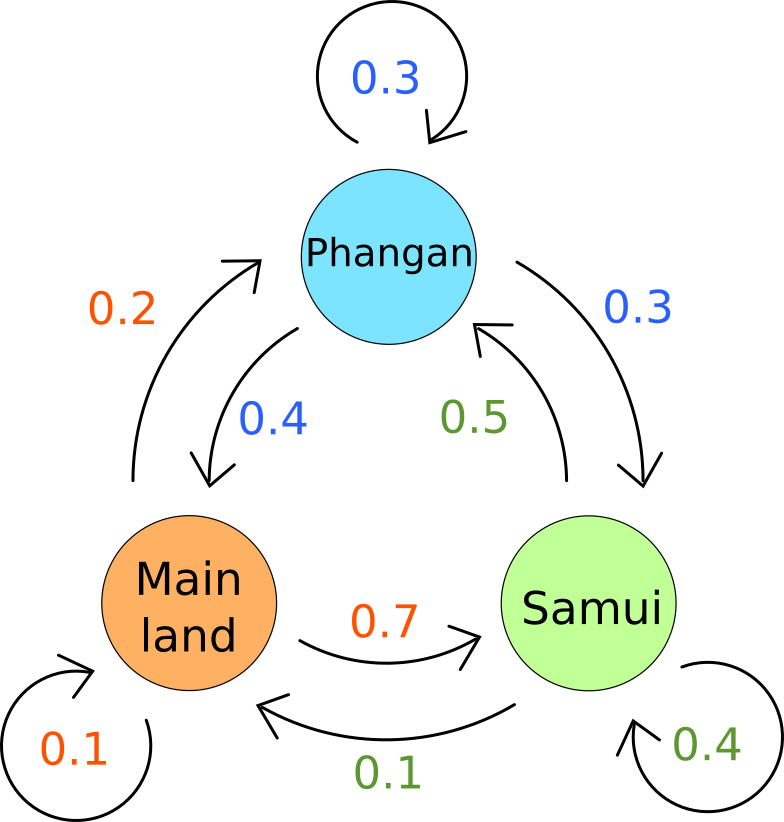
Once people arrive in Thailand, they want to enjoy the sun and beaches on 2 popular islands in the south: Samui Island & Phangan Island.
From survey data, when on the mainland, 70% of tourists plan to go to Samui Island, 20% to Phangan Island, and only 10% remain on shore the next day.
When on Samui Island, 40% continue to stay on Samui, 50% plan to go to Phangan Island, and only 10% return to mainland the next day.
Finally, when on Phangan Island, 30% prolong their stay here, 30% divert to Samui Island, and 40% go back to mainland the next day.
Starting from the mainland, what is the probability (in percentage) that the travelers will be on the mainland at the end of a 3-day trip?
The answer is 22.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Great! The Markov chain setup makes it easy to determine these probabilities through linear algebra.
A more interesting variant of this problem is to ask for the steady state.
Log in to reply
Oh, you mean probability of staying in 1 place only?
Log in to reply
Like, "If we placed 1000 retirees on the mainland, in the long run, how many of them would be in Samui?"
Then, the markov chain analysis makes this much clearer. It also helps to address the cases where we have 2 alternating steady states.
Please do explain what the 'steady state' represents? And how do I figure the answer to that question.
How and why did you pick your designations for the rows and columns? I tried changing the second column to indicate Phangan, and the third to indicate Samui, but when I did that and cubed the matrix, I got different results, though I don't see why.
Log in to reply
Are you familiar with Markov Chains ? Each row represents getting out of that island (hence sum to 1), and each column represents getting to that island from the island in the row.
Swapping the columns would not affect the end result. E.g You can think of
A
as the matrix that swaps the second and third column, then
P
p
e
t
e
r
=
A
−
1
P
A
and so
P
p
e
t
e
r
3
=
A
−
1
P
3
A
.
If you got a different result, can you post your working?
Log in to reply
Nope, that makes sense. Thank you for your help :)
C'mon you present probabilities in numbers and then you consider wrong if I answer .229. It feels like my old math teacher who enjoyed tricking us instead of teaching.
I just spent two hours trying to figure out what I was doing wrong beause I expressed the answer as a decimal, as is shown anywhere else in this article, instead of a percentage. Please fix your directions. Really wish I had those two hours of concentration back.
Trying to solve it in the most simple and boring way. Let us assume there are 1000 people who arrived at the mainland. So according to the state, at the end of day 1 the population state would be : 0.1% at Mainland = 0.1 * 1000 = 100 Simmilarly 700 and 200 at Samui and Phangan respectively.
So that becomes our transformation data for second day, applying the percentages again we get: Mainland : ( 0.1 * 100 = 10 ) + ( 0.1 * 700 = 70 ) + (0.4 * 200 = 80 ) = 160 Samui (0.7 * 100 = 70)+ (0.4 * 700 = 280) + (0.3 * 200 = 60) = 410 Phangan (0.2 100 = 20) + (0.5 700 = 350) + (0.3*200 = 60) = 430
That is our population destribution at end of day 2. And so for day 3 we have: Mainland 16 + 41 + 172 = 229
It's probably my fault of not reading properly.. but if you show probabilities in decimal, why you ask for result in percentage!? you also put the hint for 3 decimal places and for me the result was 0.229. In math probabilities are decimal numbers, percentages are for economists..
Tnks for the illustration. If the questions comes like this starting from mainland and ending at samui how do we go about it?
Log in to reply
The matrix goes (x->x x->y x->z) (y->x y->y y->z) (z->x z->y z->z)
Just keep multiplying by the number of transitions you require, then see the value at the spot based on what you require.
"most simple and boring way" = intuitive
I do not agree with the solution. Since the travelers take 1 day to decide where to go, meaning they should have been on the mainland for one full day, and thus a whole round trip could not have been achieved in 3 days, a 2-step transition should have been sufficient. What does a 3 day trip even mean here? Therefore, the answer should have been the simpler 16%, not the more complicated 22.9%.
I had the same reflection, it is more logical for the answer to be 0.16 instead of 0.229.
I do not see any words in the paragraph that say it take 1 day to decide where to go, it just said statistically when you ask travelers again the next day then we got the percentage that they stay or go. Like travelling back and forth from each place would not take more than 4-5 hours since it just an island and boat are super fast already. And i think when they said 3-days trip, it mean they want you to multiply the same matrix 3 times.
(1st day, 2nd day, 3rd day) Add all 9 possible transition probabilities
stay on main land first day, 3 possibilities ( 0 . 1 × 0 . 1 × 0 . 1 ) + ( 0 . 1 × 0 . 7 × 0 . 1 ) + ( 0 . 1 × 0 . 2 × 0 . 4 ) +
start with Samui first day, 3 possibilities ( 0 . 7 × 0 . 1 × 0 . 1 ) + ( 0 . 7 × 0 . 4 × 0 . 1 ) + ( 0 . 7 × 0 . 5 × 0 . 4 ) +
start with Phangan first day, 3 possibilities ( 0 . 2 × 0 . 4 × 0 . 1 ) + ( 0 . 2 × 0 . 3 × 0 . 4 ) + ( 0 . 2 × 0 . 3 × 0 . 1 )
= 0 . 2 2 9 = 2 2 . 9 %
For fun, I continued the process for future days, 5, 7, 9, etc. After about day 4, the probabilities that tourist will end up in each of the cities tends to stabilize no matter which city they start from. For the mainland, I have a row of ~.209; Samui: ~.426; and Phangan: ~.364.
Since obviously all the columns still sum to 1, it seems that if you stay long enough, the last day location has the same odds regardless of where you started. What kind of implications does this have in the world of Markov Chains? Does it represent what the general population of the tourists are doing, in the sense of something like "At any given time, the mainland has 20.9% of all tourists, Samui: 42.6%, and Phangan: 36.4%?" It clearly tends towards an equilibrium, I just don't know what it means for understanding what the chain is telling us.
Thanks in advance.
Let the first column of the transition matrix indicates destination of the mainland, the second indicates Samui, and the third indicates Phangan, while the rows correspond in the same fashion. Then we will write the transition matrix as: P = ⎝ ⎛ 0 . 1 0 . 1 0 . 4 0 . 7 0 . 4 0 . 3 0 . 2 0 . 5 0 . 3 ⎠ ⎞ .
For a 3 -step transition, P 3 = ⎝ ⎛ 0 . 2 2 9 0 . 2 1 1 0 . 1 9 6 0 . 4 0 5 0 . 4 3 8 0 . 4 2 5 0 . 3 6 6 0 . 3 5 1 0 . 3 7 9 ⎠ ⎞ .
Hence, starting from mainland and ending at mainland, there is a probability of 2 2 . 9 % (noted at first column and row).