Sun Embracing the Moon
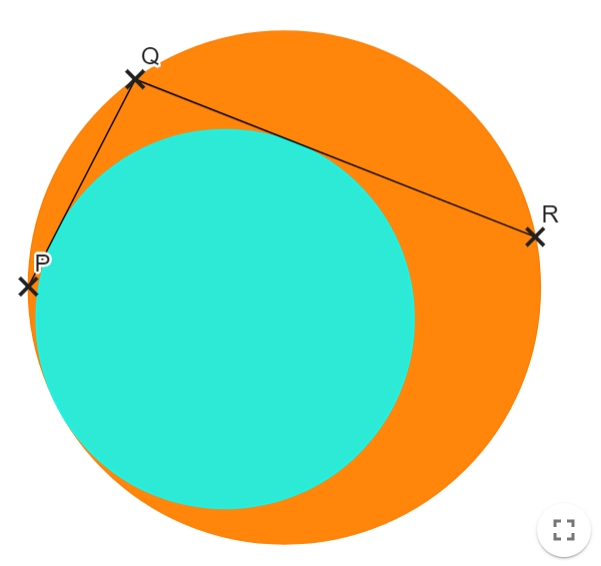
As shown above, the s m a l l e r circle is tangent to chords P Q , Q R and internally tangent to the l a r g e r circle.
If the chords P Q and Q R have chord lengths 1 4 and 4 0 respectively and the diameter of the l a r g e r circle is 5 0 . Find the radius of the s m a l l e r circle.
Let the radius of the s m a l l e r circle be r , compute your answer as 8 1 r .
This is part of the set Fun With Problem-Solving .
The answer is 1300.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Amazing solution
Let the center of the larger circle be S and draw three radii S V (the perpendicular bisector of chord P Q with intersection T ), S W (the perpendicular bisector of chord Q R with intersection U ), and S Q .
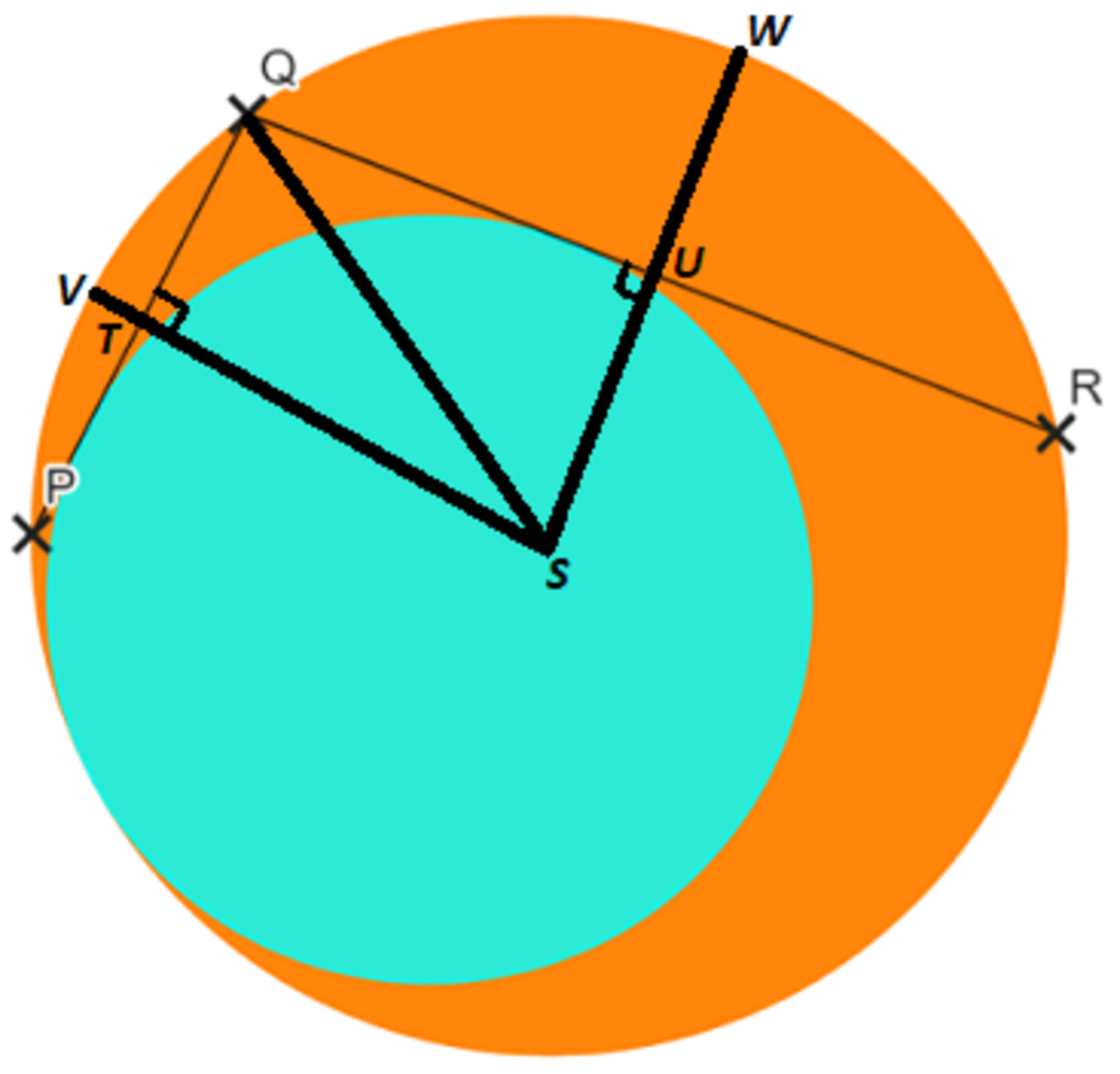
Then as radii of the larger circle, S V = S W = S Q = 2 1 5 0 = 2 5 . Also, Q T = 2 1 1 4 = 7 and Q U = 2 1 4 0 = 2 0 . By Pythagorean's Theorem, S U = 2 5 2 − 2 0 2 = 1 5 and S T = 2 5 2 − 7 2 = 2 4 , and ∠ Q S U = tan − 1 ( 1 5 2 0 ) = tan − 1 ( 3 4 ) and ∠ Q S T = tan − 1 ( 2 4 7 ) . Using the tangent angle addition formula, tan ∠ T S U = 1 − 3 4 2 4 7 3 4 + 2 4 7 = 4 4 1 1 7 , and so ∠ T S U = tan − 1 ( 4 4 1 1 7 ) .
Now let the center of the smaller circle be M and draw two radii M N (where N is the point of tangency of the small circle and chord Q R ) and M O (where O is the point of tangency of the small circle and chord P Q ).
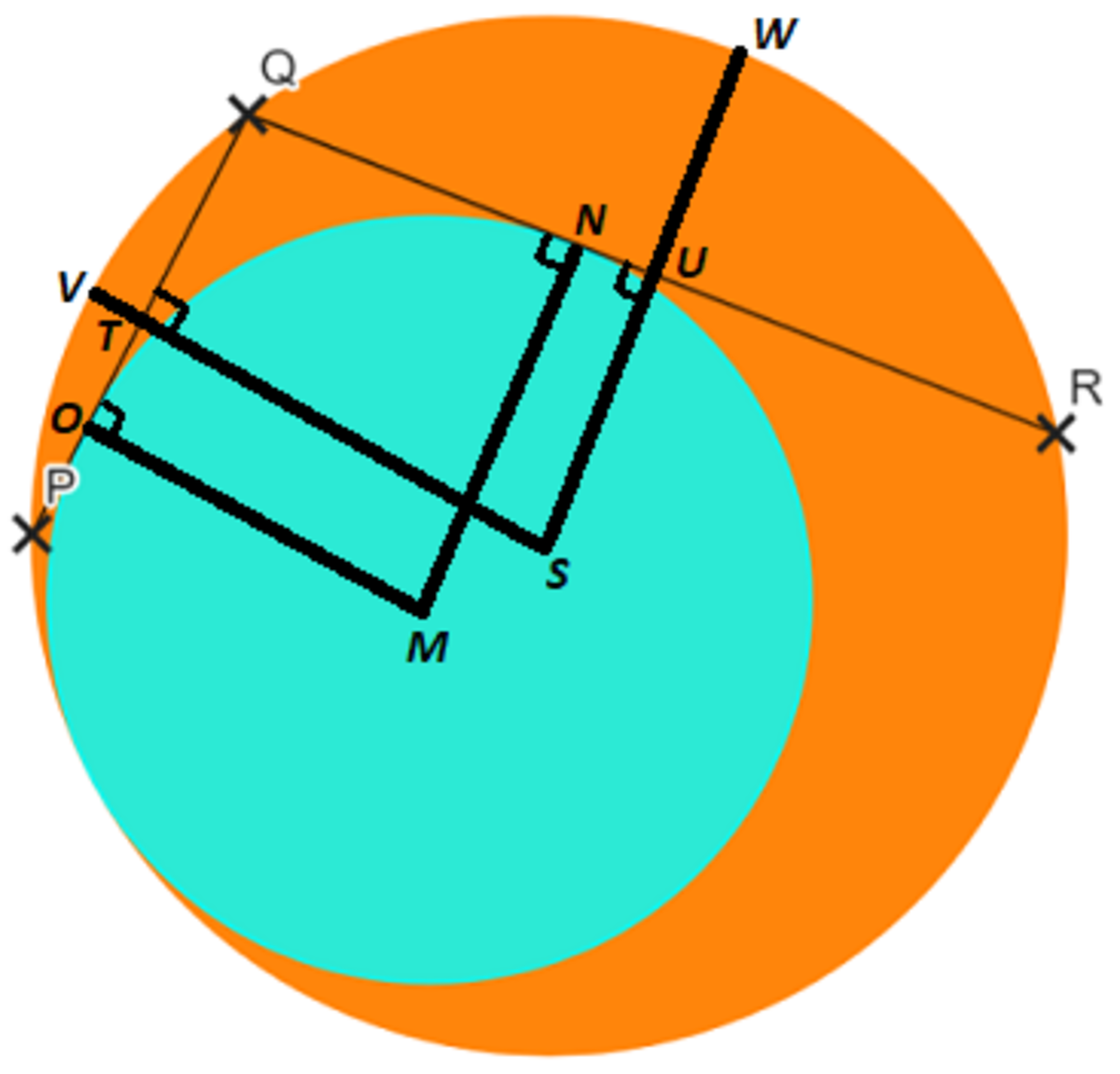
Since M N and S U are perpendicular to the same line P Q , they are parallel, and since M O and S T are perpendicular to the same line Q R , they are parallel, which means ∠ O M N = ∠ T S U = tan − 1 ( 4 4 1 1 7 ) .
Finally, let K be the point of tangency between the two circles and draw S K (through M ). Also draw M Q and S L where S L is perpendicular to M N at L .
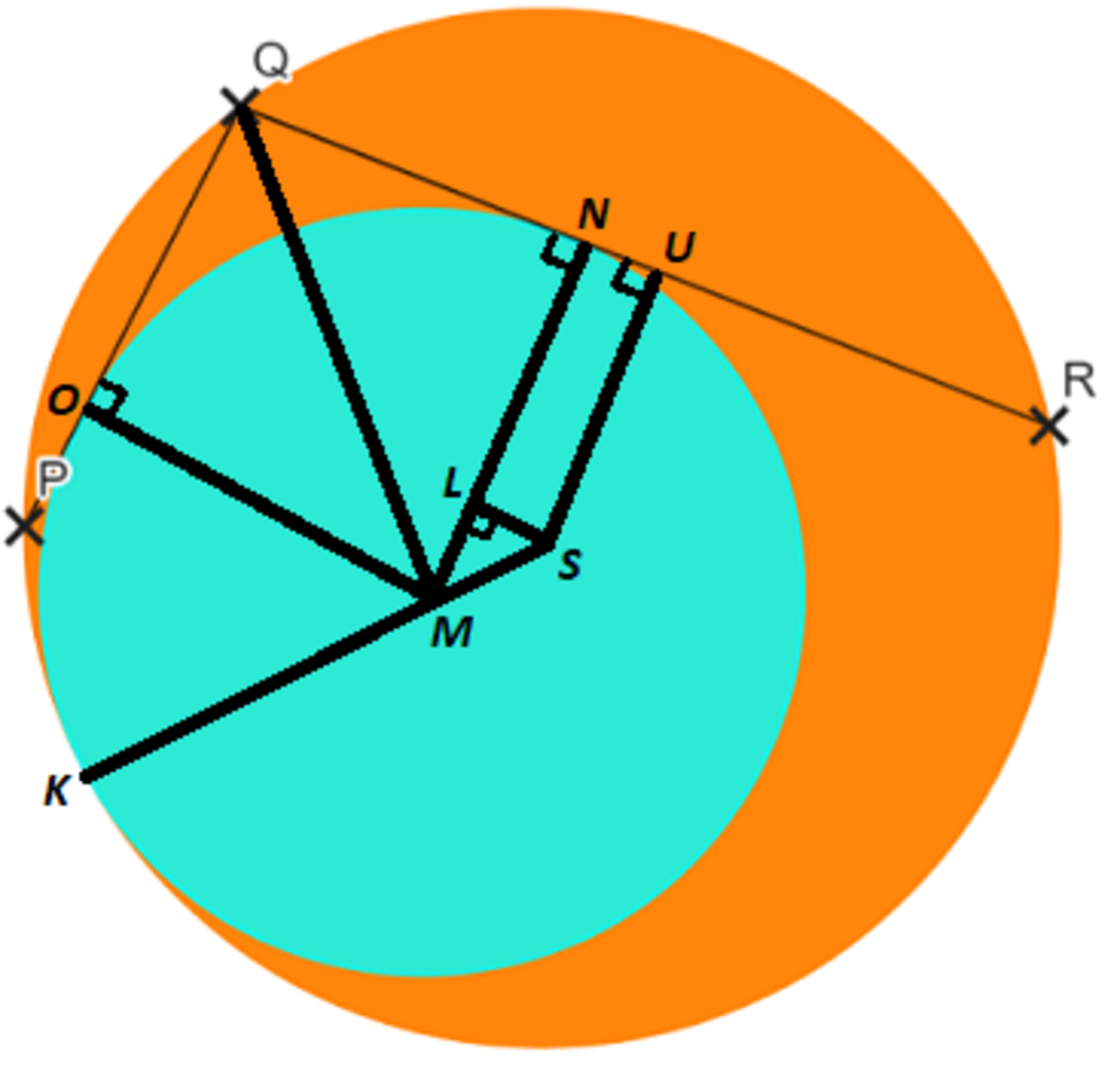
Since M O and M N are radii of circle M , M O ≅ M N , and since △ Q M O and △ Q M N are perpendicular triangles with a shared side Q M , △ Q M O ≅ △ Q M N by hypotenuse-leg congruency. Therefore, ∠ Q M N = ∠ Q M O = 2 1 ∠ O M N = 2 1 tan − 1 ( 4 4 1 1 7 ) . By tangent half angle formula, tan ∠ Q M N = tan ( 2 1 tan − 1 ( 4 4 1 1 7 ) ) = 1 + cos ( tan − 1 ( 4 4 1 1 7 ) ) sin ( tan − 1 ( 4 4 1 1 7 ) ) = 1 + 1 2 5 4 4 1 2 5 1 1 7 = 1 3 9 .
Let r be the radius of the smaller circle. Then M N = r and Q N = r tan ∠ Q M N = 1 3 9 r , and the sides of △ M L S are S M = S K − M K = 2 5 − r , L M = M N − S U = r − 1 5 , and L S = Q U − Q N = 2 0 − 1 3 9 r . Since △ M L S is a right triangle, by Pythagorean Theorem L M 2 + L S 2 = S M 2 , so ( r − 1 5 ) 2 + ( 2 0 − 1 3 9 r ) 2 = ( 2 5 − r ) 2 , and solving for r > 0 gives r = 8 1 1 3 0 0 . Therefore, 8 1 r = 8 1 ⋅ 8 1 1 3 0 0 = 1 3 0 0 .
@David Vreken great solution. Yours take a detour from the infamous cosine rule. By the way, how do you copy my image?Could u teach me?I have wanted to do so to write solution for other people's geometry questions.
Log in to reply
Thanks! To copy an image, you can either press the "prt sc" key on your keyboard (this will copy the entire screen so you will have to crop it later) or you can right click the image and choose "copy image". Once you have a the image copied, you can paste it in an image editor. I usually use Microsoft Paint in Windows.
The radius of the larger circle is 2 5
Since A C ⊥ P Q and A P = A Q ,
we have P C = C Q = 7
Similarly, Q D = D R = 2 0
cos ∠ P Q A = 2 5 7
⇒ tan ∠ P Q A = 7 2 4
cos ∠ R Q A = 2 5 2 0 = 5 4
⇒ tan ∠ R Q A = 4 3
Let ∠ P Q A = α , ∠ R Q A = β
⇒ tan α = 7 2 4 , tan β = 4 3
tan ( α + β ) = 1 − 7 2 4 ⋅ 4 3 7 2 4 + 4 3 = − 4 4 1 1 7
Let α + β = 2 γ
⇒ tan ( α + β ) = tan 2 γ
1 − ( tan γ ) 2 2 tan γ = − 4 4 1 1 7
− 8 8 tan γ = 1 1 7 − 1 1 7 ( tan γ ) 2
1 1 7 ( tan γ ) 2 − 8 8 tan γ − 1 1 7 = 0
( 1 3 tan γ + 9 ) ( 9 tan γ − 1 3 ) = 0
tan γ = − 1 3 9 or tan γ = 9 1 3
∵ 0 < γ < 2 π
∴ tan γ > 0
∴ tan γ = − 1 3 9 is unsuitable
∴ tan γ = 9 1 3
∠ P Q F = ∠ F Q R = γ
∴ tan ∠ P Q F = 9 1 3
sin ∠ P Q F = 1 3 2 + 9 2 1 3 = 2 5 0 1 3 = 5 1 0 1 3
sin ∠ P Q F = Q F r
∴ Q F r = 5 1 0 1 3
Q F = 1 3 5 1 0 r
Q A = 2 5
∵ the two circles are internally tangent
∴ the two centers A , F and the tangent point E are collinear.
∴ F A = 2 5 − r
∠ F Q A = α − γ
tan ∠ F Q A = tan ( α − γ ) = 1 + tan α tan γ tan α − tan γ = 1 + 7 2 4 ⋅ 9 1 3 7 2 4 − 9 1 3 = 3 7 5 1 2 5 = 3 1
cos ∠ F Q A = 1 2 + 3 2 3 = 1 0 3
By Cosine Rule ,
( 2 5 − r ) 2 = ( 1 3 5 1 0 r ) 2 + 2 5 2 − 2 ⋅ 1 3 5 1 0 r ⋅ 2 5 ⋅ 1 0 3
( 2 5 − r ) 2 = 1 3 2 2 5 0 r 2 + 2 5 2 − 1 3 7 5 0 r
1 6 9 ( 2 5 − r ) 2 = 2 5 0 r 2 + 2 5 2 ⋅ 1 6 9 − 7 5 0 r ⋅ 1 3
1 6 9 r 2 − 1 6 9 ⋅ 5 0 r + 1 6 9 ⋅ 2 5 2 = 2 5 0 r 2 + 2 5 2 ⋅ 1 6 9 − 7 5 0 r ⋅ 1 3
1 6 9 r 2 − 1 6 9 ⋅ 5 0 r = 2 5 0 r 2 − 7 5 0 r ⋅ 1 3
8 1 r 2 + ( 1 6 9 ⋅ 5 0 − 7 5 0 ⋅ 1 3 ) r = 0
8 1 r 2 + 1 3 ⋅ 5 0 ( 1 3 − 1 5 ) = 0
8 1 r 2 − 2 ⋅ 1 3 ⋅ 5 0 = 0
8 1 r 2 − 1 3 0 0 r = 0
r ( 8 1 r − 1 3 0 0 ) = 0
r = 0 or r = 8 1 1 3 0 0
∵ r > 0
∴ r = 0 is unsuitable
r = 8 1 1 3 0 0
8 1 r = 1 3 0 0