Sunligth on the lake bottom
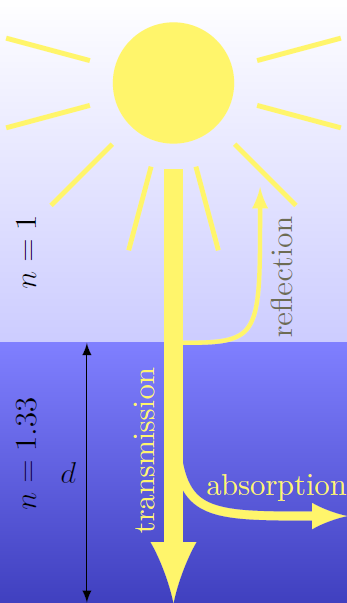
At noon on the summer solstice on the equator, the sun is at its zenith. The sunlight shines on a crystal clear lake with the depth What is the relative light intensity of the sun's rays reaching the bottom of the water? Here, denotes the intensity of the incident sunlight. Returns the result in percent and rounds it to the nearest integer.
Assumptions: Water has a refractive index of , whereas for the air we can assume . At a depth of the intensity of the transmitted light decreases by half by absorption.
Hint: You can solve this problem with the help of the Fresnel equations, but for real challenge you can also derive the solution from the scratch: For light of wavelength , the incident light beam has an electric field of the form with the freqeuncy , the wave number and light velocity . The total electric field has the form with the contributions and of the reflected and transmitted beams. Find a solution for which functions and can be continued steadily at (water surface) . The intensity of the light is calculated according to .
The answer is 74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the water wave number and wave length change according to k ′ = n k and λ ′ = λ / n . Furthermore, absorption causes an exponential decay E ( t ) ∝ e α z of the transmitted beam. The decay coeffizient α is determined by I ( 0 ) I ( − d 0 ) = e − 2 α d 0 = 2 1 ⇒ α = 2 d 0 lo g 2 = 0 . 0 3 5 m 1 Therefore, the electric field can be written as E ( z , t ) = { E 0 e i ( ω t + k z ) + A e i ( ω t − k z ) B e i ( ω t + n k z ) e α z z > 0 z < 0 with unknown coefficients A and B . The connection condition for the water surface results to E ( z = 0 , t ) E ′ ( z = 0 , t ) = ( E 0 + A ) e i ω t = B e i ω t = i k ( E 0 − A ) e i ω t = ( i n k + α ) B e i ω t ≈ i n k B e i ω t In the last line α was neglected, because the eletric field changes only slightly by the absorption on the long scale of a wavelength ( λ ≪ d 0 or k ≫ α ). Therefore, a system of linear equations results ( − 1 1 1 n ) ( A B ) ⇒ ( A B ) = ( E 0 E 0 ) = 1 + n − 1 ( n − 1 − 1 − 1 ) ( E 0 E 0 ) = 1 + n E 0 ( 1 − n 2 ) The light intensity on the lake bottom results I ⇒ I 0 I = 2 1 c ε ε 0 ∣ E ( − d ) ∣ 2 = 2 1 n c 0 ε 0 ∣ B ∣ 2 e − 2 α d = ( 1 + n ) 2 4 n e − 2 α d I 0 = ( 1 + n ) 2 4 n e − 2 α d ≈ 0 . 7 4 1 with the Intensity I 0 = 2 1 c 0 ε 0 ∣ E 0 ∣ 2 .of the incident light.