Super Duper Star!

Geometry Level 3

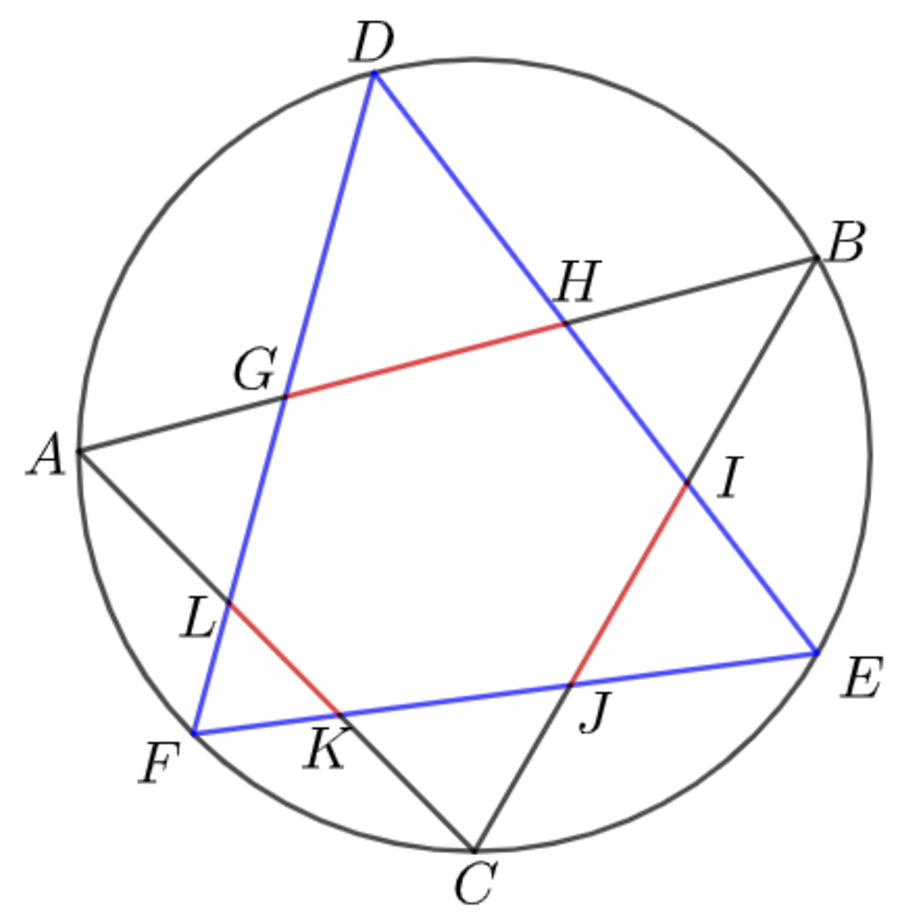
In the circumcircle, containing the nondegenerate triangle △ A B C \bigtriangleup ABC , points D , E , F D,E,F are the midpoints of arcs A B AB , B C BC and A C AC , respectively, which altogether form the blue triangle △ D E F \bigtriangleup DEF . The intersection points G , H , I , J , K , L G,H,I,J,K,L are formed. Which of the following statements below is/are true?

( 1 ) (1) If △ A B C \bigtriangleup ABC is equilateral, then all red segments have congruent lengths. That is: ∣ G H ‾ ∣ = ∣ I J ‾ ∣ = ∣ K L ‾ ∣ |\overline{GH}| = |\overline{IJ}| = |\overline{KL}| .

( 2 ) (2) If ∣ G H ‾ ∣ = ∣ I J ‾ ∣ = ∣ K L ‾ ∣ |\overline{GH}| = |\overline{IJ}| = |\overline{KL}| , then △ A B C \bigtriangleup ABC is equilateral.

Only ( 1 ) (1) is true. Only ( 2 ) (2) is true. Both ( 1 ) (1) and ( 2 ) (2) are true. Neither ( 1 ) (1) nor ( 2 ) (2) is true.

Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Jake Ibrahim
Mar 3, 2021

  • 1)-true- We should begin by finding the center. You have to bisect each side of ABC . Now because DEF is formed using the midpoints of the arcs made by ABC we know DEF is equilateral because if you connect the endpoints of ABC to the center the angles made are 120 degrees because of Euclid book 3 prop 20. now if we connect the endpoints of DEF to the center the angles made are half the 120 degree angles so they are 60 degrees but if you recombine them with the other 60 degrees you get an equilateral triangle

  • 2)-true-using the diagram from number one the shape when connecting all the intersection points is a hexagon where we can prove all the sides are equal using SAS meaning that GH =IJ = KL

This is my first proof so can you give some feedback on the format and quality of the proof etc.

0 Helpful 0 Interesting 0 Brilliant 1 Confused

For number 2, you took that for granted that the triangle is an equilateral by SAS property. How do we know those triangles follow SAS property (How is that obvious)? Note that to prove that true, you can't assume at first △ A B C \bigtriangleup ABC is equilateral as you did for number 1 (logic-wise). If suppose we want to consider ∣ G H ‾ ∣ = ∣ I J ‾ ∣ = ∣ K L ‾ ∣ |\overline{GH}| = |\overline{IJ}| = |\overline{KL}| as the given assumption, we work from there.

Michael Huang - 3 months, 1 week ago

alright thank you for the feedback, other than that does number 1 look good

Jake Ibrahim - 3 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...