Super + Ellipse = Super Ellipse!

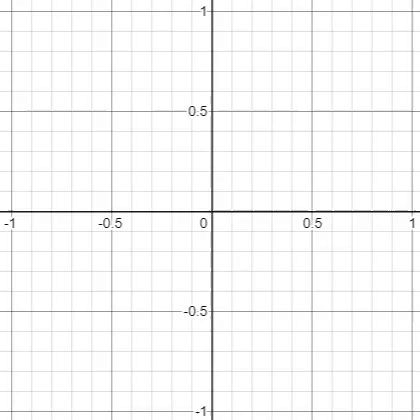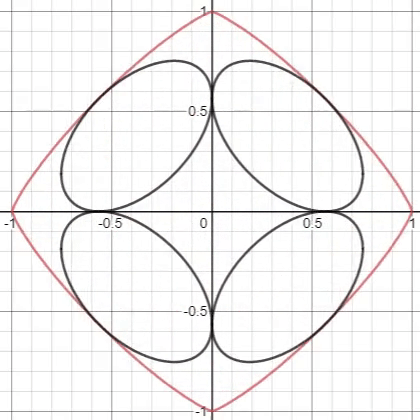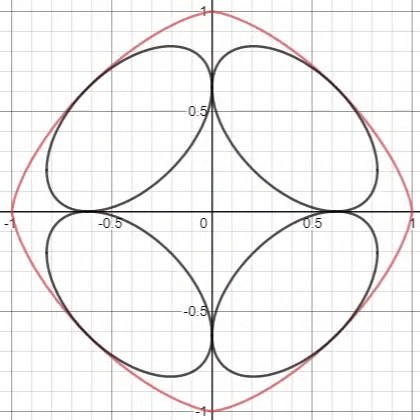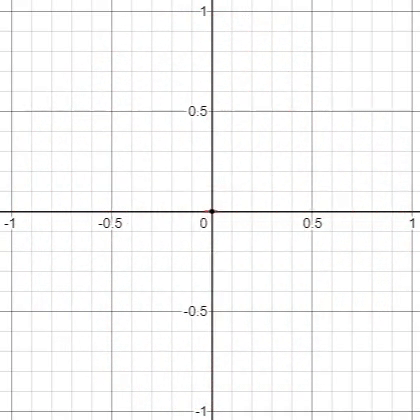
The above animation shows the maximum packing of the ellipse bounded by two axes in the superellipse of the equation $|x|^n + |y|^n = 1$ . If the maximum total area ratio of the inscribed ellipses to the superellipse for $0 < n \leq 2$ is $A$ , input $\lfloor 10^5 A\rfloor$ as your answer.

---

For Fun. For $n \geq 1$ , generalize the critical (maximum possible) eccentricity value of centrally-positioned ellipses, such that either their major axes or their minor axes each share one common point of tangency with the superellipse at $y = x$ or $y = -x$ .

---

Inspiration.