Super Geometry Problem
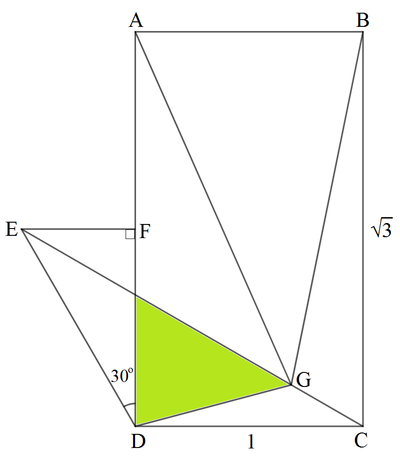
As shown in the figure, A B C D is a rectangle with side lengths of 1 and 3 . △ A B G has an area of 2 2 9 3 , △ D E F has an area of 8 3 , ∠ E D F = 3 0 ∘ and E F is perpendicular to A D .
If the area shaded green is given by b 5 a , where a and b are integers with a being square-free. Find a + b .
The answer is 69.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Congrats on being the first to produce a solution! 🎉
My idea is that this can be shown to be part of a regular hexagon.
@Brilliant Mathematics , or who ever edited the problem for me, could you tell me what software you used to produce the diagram. Thank you.
Log in to reply
Hi Barry, I believed @Chew-Seong Cheong has updated the image in the problem statement.
I redid the image for you. I used Desmos for the lines and Paint to get in the labels and numbers.
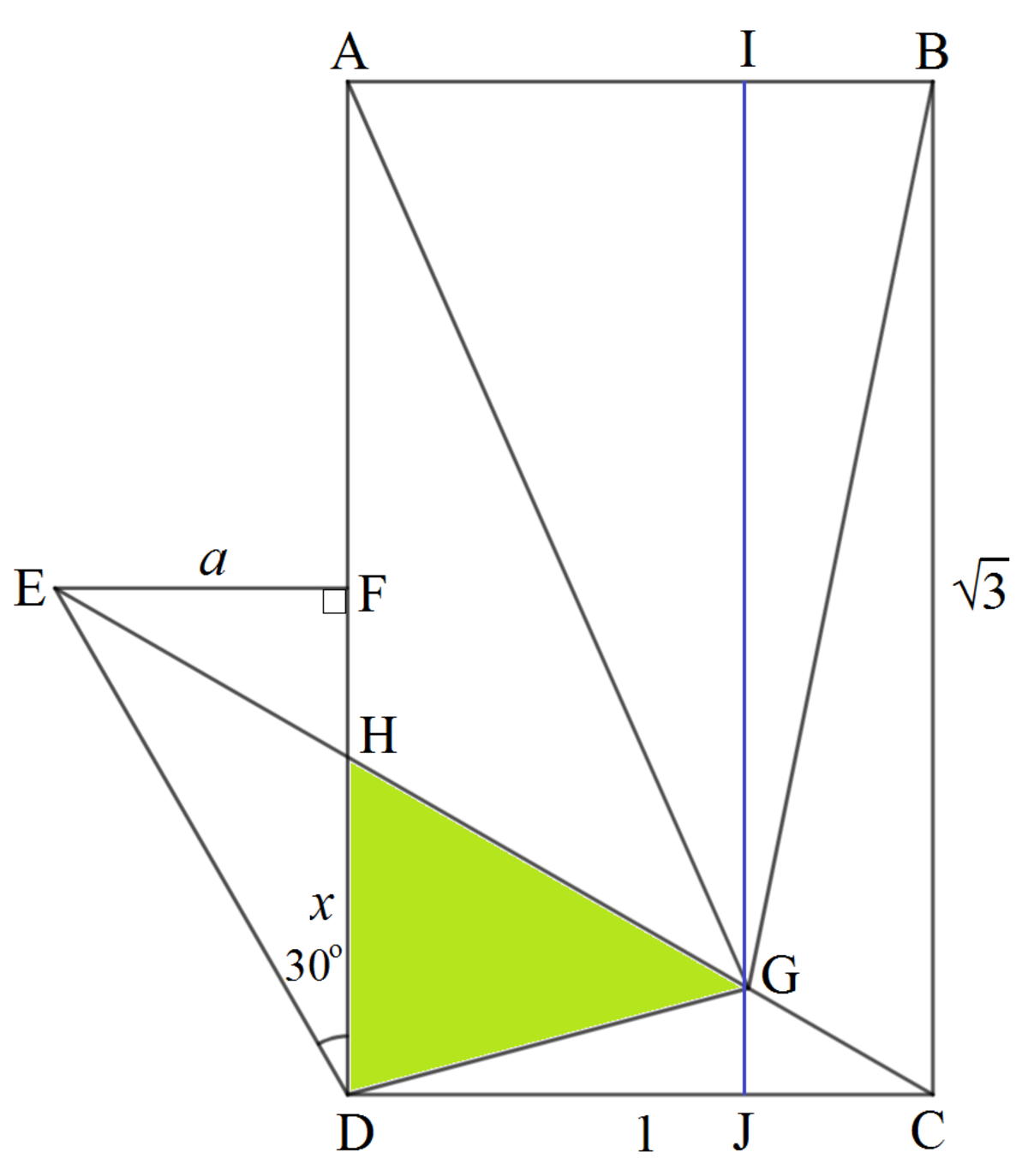
Let E F = a . Then D F = a cot 3 0 ∘ = 3 a . Since the area of △ D E F is 2 a ⋅ 3 a 8 3 ⟹ a = 2 1 = E F and D E = 2 3 .
Let the intersection point of A D and C E be H and D H = x . Then F H = 2 3 − x . We note that △ E F H and △ C D H are similar. Then D H F H = C D E F ⟹ x 2 3 − x = 2 1 ⟹ x = 3 1 = 3 3 .
Draw I J parallel to B C . Since the area of △ A B G is 2 I G ⋅ 1 = 2 2 9 3 ⟹ I G = 1 1 9 3 . Then G J = I J − I G = 3 − 1 1 9 3 = 1 1 2 3 .
Now area of the green triangle is
[ D G H ] = [ C D H ] − [ C D G ] = 2 D H ⋅ C D − 2 G J ⋅ C D = 6 3 − 1 1 3 = 6 6 5 3
Therefore a + b = 3 + 6 6 = 6 9 .
@Barry Leung , you have to mention that a is square-free because 6 6 5 3 = 1 3 2 5 1 2 = 1 9 8 5 2 7 = ⋯ . Infinitely many solutions again.
Mark the letters M and N , we find S △ A B N + S △ C D N = 2 1 S A B C D (You can see a beautiful proof about it at the bottom).
So S △ C D N = 1 × 3 − 2 2 9 3 = 1 1 3 .
And because of E F ⊥ A D , ∠ E D F = 3 0 ∘ and S △ D E F = 8 3 , so we can know E F = 2 1 , F D = 2 3 .
In addition, we can find △ E F M ∼ △ C D M , so we assume D M = x , so:
2 1 : ( 2 3 − y ) = 1 : y
y = 3 3
So S △ C D M = 3 3 × 1 × 2 1 = 6 3 .
and so
S △ D M N = 6 3 − 1 1 3 = 6 6 5 3
So a = 3 , b = 6 6 , the answer is:
3 + 6 6 = 6 9
Beautiful Proof: