Super Smash Ball
In the following diagram, b − a = 5 0 , d − c = 7 8 , and a , b , c , d , and the radius of the circle are all integers.
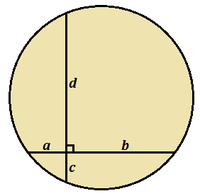
Find the radius of the circle.
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice use of coordinate geometry! A friend showed me a theorem I hadn't seen before that a 2 + b 2 + c 2 + d 2 = 4 R 2 , which I was trying to highlight with this question and used in my own solution.
From the intersecting chords theorem , a b = c d , and from this theorem we know that a 2 + b 2 + c 2 + d 2 = 4 R 2 .
Now a b = c d rearranges to b = a c d and b − a = 5 0 rearranges to b = a + 5 0 , so b = a c d = a + 5 0 , which solves to a = c d + 6 2 5 − 2 5 , so that b = a + 5 0 = c d + 6 2 5 + 2 5
Also, d − c = 7 8 rearranges to d = c + 7 8 , so that a = c d + 6 2 5 − 2 5 = c 2 + 7 8 c + 6 2 5 − 2 5 and b = c d + 6 2 5 + 2 5 = c 2 + 7 8 c + 6 2 5 + 2 5 .
Substituting a = c 2 + 7 8 c + 6 2 5 − 2 5 , b = c 2 + 7 8 c + 6 2 5 + 2 5 , and d = c + 7 8 into a 2 + b 2 + c 2 + d 2 = 4 R 2 gives ( c 2 + 7 8 c + 6 2 5 − 2 5 ) 2 + ( c 2 + 7 8 c + 6 2 5 + 2 5 ) 2 + c 2 + ( c + 7 8 ) 2 = 4 R 2 , which rearranges to R 2 − ( c + 3 9 ) 2 = 6 2 5 .
Letting k = c + 3 9 , we have R 2 − k 2 = 6 2 5 for integers R and k , or ( R − k ) ( R + k ) = 6 2 5
Out of the factors of 6 2 5 , R − k can be either 1 or 5 .
If R − k = 1 , then R + k = 6 2 5 , R = 3 1 3 , k = 3 1 2 , c = 2 7 3 , and a = 8 1 5 0 7 − 2 5 , a non-integer. Therefore, R − k cannot be 1 and must be 5 .
If R − k = 5 , then R + k = 1 2 5 , R = 6 5 , k = 6 0 , a = 2 7 , b = 7 7 , c = 2 1 , and d = 9 9 , the only integer solution.
Therefore, R = 6 5 .
That's a really nice theorem! I think it's possible to get into the number theory part of it without the big square roots; starting from a 2 + b 2 + c 2 + d 2 = 4 R 2 and a b = c d , we get a 2 − 2 a b + b 2 + c 2 + 2 c d + d 2 2 5 0 0 + ( c + d ) 2 6 2 5 + ( 2 c + d ) 2 6 2 5 + ( 2 c + c + 7 8 ) 2 6 2 5 + ( c + 3 9 ) 2 = 4 R 2 = 4 R 2 = R 2 = R 2 = R 2
...and the rest is Pythagoras.
Log in to reply
That's really clever! I wish I had thought of that! Thanks for sharing!
Very clever solution and the theorem too! I am amazed on how elegant that is
Take the two chords as coordinate axes. The centre of the circle lies on the intersection of the perpendicular bisectors of the two chords.
The circle intersects the horizontal axis at ( − a , 0 ) and ( b , 0 ) . The midpoint of this chord is therefore at ( 2 a + b , 0 ) , ie ( 2 5 , 0 ) ; so its perpendicular bisector has equation x = 2 5 . Similarly, the perpendicular bisector of the vertical chord is y = 3 9 , so the centre of the circle has coordinates ( 2 5 , 3 9 ) .
Now, any circle with this centre big enough to intersect the axes will satisfy the conditions b − a = 5 0 and d − c = 7 8 , so we need to use the fact that a , b , c , d and r (the radius of the circle) are integers.
The equation of the circle is ( x − 2 5 ) 2 + ( y − 3 9 ) 2 = r 2 . Since the point ( 0 , − c ) is on the circle, 2 5 2 + ( c + 3 9 ) 2 = r 2
This is a Pythagorean triple! So, for some positive integers m , n , t with m and n coprime, t ( m 2 − n 2 ) = 2 5 ; 2 t m n = c + 3 9 ; t ( m 2 + n 2 ) = r 2
We only need the first of these, ie t ( m 2 − n 2 ) = 2 5 to see there are just two possible solutions; ( m , n , t ) = ( 3 , 2 , 5 ) which gives r = 6 5 or ( m , n , t ) = ( 1 3 , 1 2 , 1 ) , giving r = 3 1 3 .
In the same way, since the point ( − a , 0 ) lies on the circle, ( a + 2 5 ) 2 + 3 9 2 = r 2
Now, 3 1 3 2 − 3 9 2 = 9 6 4 4 8 , which is not a square number. But 6 5 2 − 3 9 2 = 2 7 0 4 = 5 2 2 , so we find r = 6 5 .
The rest of the lengths are ( a , b , c , d ) = ( 2 7 , 7 7 , 2 1 , 9 9 ) .