Superb Circular Shapes
In this problem I asked your attention for the curve S : 1 − ∣ x ∣ + 1 − ∣ y ∣ = 1 , which looks a lot like a circle but bulges just a little. It is easy to check that this curve runs through the points ( 0 , ± 1 ) , ( ± 1 , 0 ) , as well as ( ± 4 3 , ± 4 3 ) .
As someone pointed out, this has to do with superellipses --but curve S is not actually a superellipse. However, there exists a superellipse that is very similar to our shape, given by T : ∣ x ∣ n + ∣ y ∣ n = 1 (with n a real parameter), which runs through the same eight points ( 0 , ± 1 ) , ( ± 1 , 0 ) , as well as ( ± 4 3 , ± 4 3 ) .
A section of both curves is shown in the diagram above: the blue graph is curve S , and the orange graph the superellipse T .
Clearly, the nearly circular area included by T is slightly larger than that included by S . How much bigger is it, expressed as a percentage?
Notes:
- Give your answer as a percentage with three decimals precision.
- This problem requires numerical integration. (If you can find a different solution, I am very interested!)
The answer is 0.367.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I got AT ~ 0.854178, with 2.504% difference. I used the online free version of Wolfram alpha to compute this value.
Log in to reply
Log in to reply
Yeah I was wrong, messed up the integral somewhere.
Nice problem,approx 11/30 %
(If you can find a different solution, I am very interested!)
Not sure if this helps, but.... The integral simplifies to a Beta function , n 1 ⋅ Γ ( 2 n + 2 ) ( Γ ( n + 1 ) ) 2 . Apply the recurrence formula for the Gamma function , and we just need to approx Γ ( Q ) , where 0 < Q < 1 , which is a much simpler approximation to deal with.
Log in to reply
Almost. The area is ∫ 0 1 ( 1 − x n ) n 1 d x = n 1 B ( n 1 , n 1 + 1 ) = 2 n Γ ( n 2 ) Γ ( n 1 ) 2
We limit the areas to the first quadrant.
The area included by curve S can be expressed in closed form; it is equal to A S = 5 / 6 . See my solution here for the details.
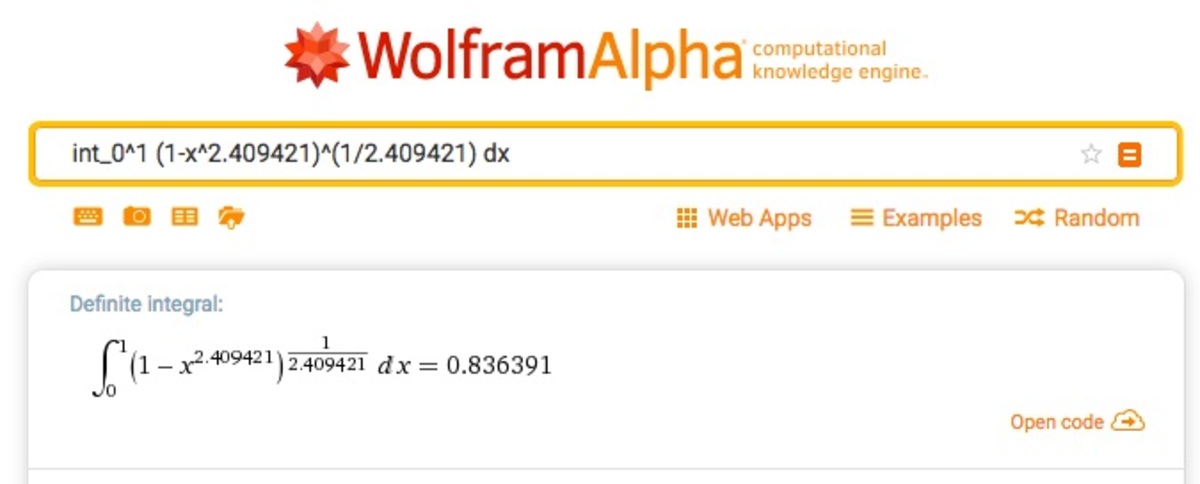
The area included by curve T is found by integration, A T = ∫ 0 1 ( 1 − x n ) 1 / n d x . To find the value of n , note that the graph passes through ( x , y ) = ( 4 3 , 4 3 ) , which requires that ( 4 3 ) n = 2 1 ∴ n = lo g 3 / 4 lo g 1 / 2 ≈ 2 . 4 0 9 4 2 1 . Performing the integration numerically we get A T ≈ 0 . 8 3 6 3 9 1 . This is about 0 . 3 6 7 % larger than A S .