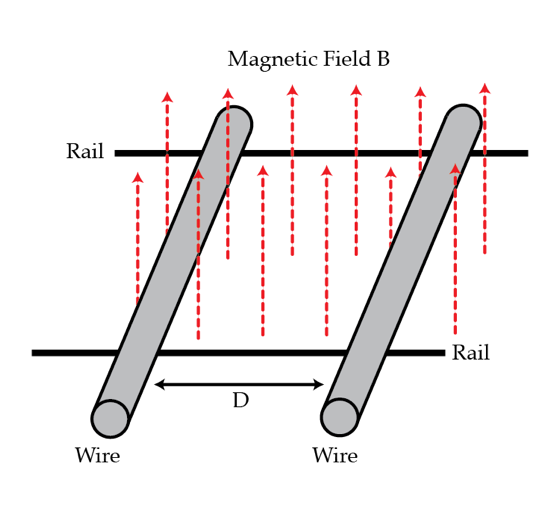
Superconducting rails and magnetic friction

Assume $l$ is the distance between two rails. The appearance of the magnetic field give each wire an initial momentum towards each other as follows: $P_{i}=\int F \mathrm{d}t = \int Bli \mathrm{d}t = \int Bl\times \frac{Dl}{2R}\times \frac {dB}{dt}\mathrm{d}t=\frac{Dl^2}{2R}\int B\mathrm{d}B=\frac{B^2l^2D}{4R}$

Lorentz forces applied on the wires slow them down: $m\frac{dv}{dt}=Bli=Bl\times \frac {Bl}{2R}\times \frac{dD}{dt}=\frac {B^2l^2}{2R} \times \frac{dD}{dt} (1)$

Intergrate both side of equation $(1)$ from $(mv_{i}=P_{i}=\frac{B^2l^2D}{4R};D_{i}=D)$ to $(mv_{f}=0;D_{f})$ : $-\frac{D}{2}=D_{f}-D$

Finally $D_{f}=\frac{D}{2}=35(cm)$

Cause the process of switching on the magnetic field happens very fast, we can ssume that the wires does not move during this process, we have: $I = \frac {\epsilon}{2R} = - \frac {D_0 l \frac {dB}{dt}} {2R}$

$\Rightarrow m \frac {dv}{dt} = BIl = - \frac {D_0 l^2}{2} \frac {B dB}{dt}$

So the velocity $v_0$ of the wires right after the macnetic field reaches value of B is: $v_0 = - \frac {D_0 l^2 B^2}{4mR}$

Next, the wires move under the effect of macnetic field:

$m \frac{dv}{dt} = B \frac{\epsilon}{2R} l = - B \frac{Bvl}{2R} l$ (1)

We also have $2v = - \frac {dD}{dt}$
(2) From (1) and (2): $\Delta D = \frac{D_0}{2}$

Finally we have the distance between the wires is $\frac{D_0}{2} = 35cm$

The inward force on the wires of a conducting loop relate to the change in external magnetic flux.

Initially, the magnetic field is considered 0. Therefore, the flux within the area of the perfectly conducting loop is $B*A=0$ .

When a magnetic field B is suddenly switched on, the new flux is equal $B*A$ . In order to balance this change in flux, the wires must move to generate an opposite flux until reaching a final flux of 0. Because the wires and rails are frictionless, superconducting, and rigid, we can assume that there are no other forces in the system to consider aside from the lateral force on the wires.

First, let the length of each wire be given by L, and assume the system remains rectangular due to the uniform force exerted on each wire. Since B is considered uniform and constant, the change in flux due to the wires moving inward may be given by: $B*A' - B*A''=B*(A'-(A-A'))$ , where $A=L*70$ cm is the original area formed by the wires and rails, $A'=L*D$ is the final area formed by the wires and rails, and A'' is the change in area: $A''=A - A'$ .

Therefore,

$B*L*( D - (70 cm -D) )=0$

Solving this equation for D, $B*L*(2D - 70 cm) = 0$ . Assuming that B and L are nonzero constants, $(2D - 70 cm)=0$ . Therefore D=35 cm.

Conceptually, the wires generate an opposing flux by creating a decreasing flux inside the loop and an equal and opposite increasing flux outside the loop. This is why the wires only need to move halfway towards each other to balance the total flux.