Support Beams
A roof with an incline rests its lower end on a horizontal beam. It is supported by 23 equally spaced, increasingly tall vertical beams which also rest on the horizontal beam. The tallest beam is 4 meters high and rests on the horizontal beam at a point 5 meters from the lower end of the roof. Find the sum of the heights of the vertical beams (in meters).
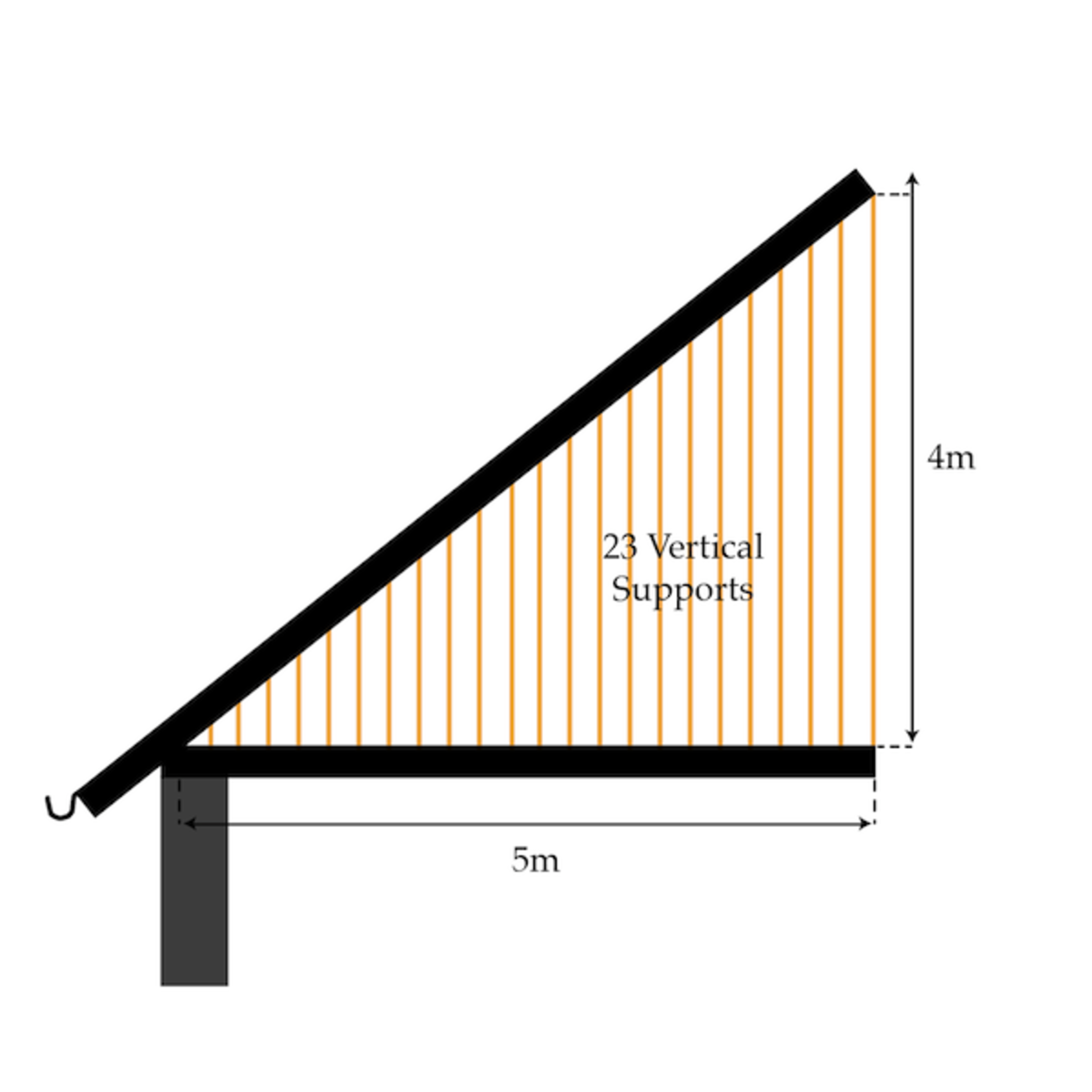
The answer is 48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is possible to see that, from the dimensions given:
tan θ = 5 4 where θ is the angle between the two lines.
Since the bottom 5m is split into 23 intervals, each interval must be 2 3 5 m long. It is better to consider the distance from the vertical support to the point where the two lines meet, and this distance is given by 2 3 5 n where n is a number from 1 to 23. The length of support x n is given by 2 3 5 n × 5 4 = 1 1 5 2 0 n (since opposite = adjacent × tan θ .
The total heights of all the supports is therefore ∑ n = 1 2 3 1 1 5 2 0 n = 1 1 5 2 0 ∑ n = 1 2 3 n .
Therefore:
Total height (metres) = 1 1 5 2 0 × 2 2 3 ( 2 3 + 1 ) = 4 8
Interestingly, this can be simplified to give:
Total height = 2 a ( b + 1 ) where a = height of the tallest support and b = the number of divisions (supports). Therefore, the total height is independent of the width over which the supports are spread (the 5m was not needed for this problem).