Supporting a Circle
A wire is in the shape of a unit circle centered on the origin, with the portion from to missing (see image). The wire's mass is , and gravity is in the direction.
A force is applied normally to the curve at all points on the curve, such that each unit of curve length experiences an infinitesimal force of the same magnitude:
In the above equation, the units on are . If the applied force keeps the wire in stasis, what is the value of ?
Note: My intent is to describe a constant linear pressure over the curve length
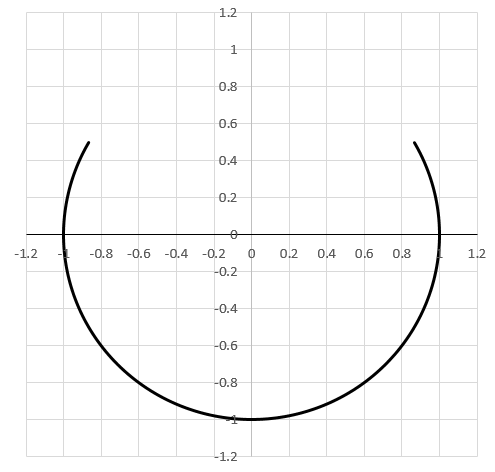
The answer is 5.7735.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
You take an element of length d l and present at angle θ from the negative y axis. Now d l = r d θ . (r=1)
The upward force on this element would be d F c o s θ . Putting d F = α d l and integrating the upward force from 0° to 120°, doubling that to count in the second half, and equalling that to m g , would give us the value of α = √ 3 1 0 .