Supporting the sin
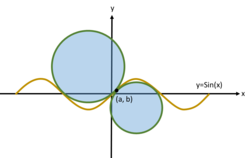 Refer to the image above (not drawn to scale)
Refer to the image above (not drawn to scale)
The 2 circles above are tangent to the graph y = sin ( x ) . The two circles share 1 point of tangency ( a , b ) , and the ratio of the area of the smaller circle to the area of the bigger circle is 4 1 .
Given that there are two possible values for b , ( b 1 and b 2 ), and that b 1 > b 2 , and that the sum of the area of both the circles can be expressed as A , find ⌊ 1 0 0 0 0 ( A + ( b 1 − b 2 ) ) ⌋
Congratulate yourself after you solve this
The answer is 411933.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
For so long there hasn't been a solver.
Anyway, here's the solution:
So if a circle is tangent to a line, the normal of that line (at the point of tangency) would pass right through the center of the circle. So to find the answer it is obvious that we have to find the gradient of y = sin ( x ) .
The plan is to find the radius of the circle in terms of b .
Consider this
 hi
hi
z = π − 2 arcsin ( b ) k = π + 2 arcsin ( b )
Now lets focus on the circle fitting inside z , with radius R
Gradient at x = arcsin ( b ) is cos ( arcsin ( b ) )
 hi
hi
Using the gradient above you can find that θ = 2 π − arctan ( cos ( arcsin ( b ) ) )
And with some more simple trigonometry you can finally express R in terms of z
R = 2 cos ( θ ) z = 2 cos ( 2 π − arctan ( cos ( arcsin ( b ) ) ) ) π − 2 arcsin ( b )
Now, doing the same on the circle fitting inside k , with radius r , we would find that
r = 2 cos ( θ ) k = 2 cos ( 2 π − arctan ( cos ( arcsin ( b ) ) ) ) π + 2 arcsin ( b )
The question asks for 2 circles with area ratio 4 1 , so the radius ratio would be 2 1 . So to find b :
r = 2 R 2 cos ( 2 π − arctan ( cos ( arcsin ( b ) ) ) ) π + 2 arcsin ( b ) = cos ( 2 π − arctan ( cos ( arcsin ( b ) ) ) ) π − 2 arcsin ( b ) π + 2 arcsin ( b ) = 2 ( π − 2 arcsin ( b ) ) b = 2 1
Note that b can also be − 2 1 which settles b 1 and b 2
Plugging b = 2 1 to find r and R to find the answer would give
⌊ 1 0 0 0 0 ( A + ( b 1 − b 2 ) ) ⌋ = 4 1 1 9 3 3
This is probably the craziest solution I wrote, I took a whole full hour.
Oh Shit, Oh no I lost my 400 points by a simple silly mistake rather than putting 2 1 and 2 − 1 I put 6 π and 6 − π
Its very good problem. Explicitly A = 2 7 3 5 π 3 , points of contact being at ± 6 π
By symmetry, let equations be
( x − 2 π ) 2 + ( y − c ) 2 = r 2 a n d ( x + 2 π ) 2 + ( y − d ) 2 = 4 r 2
Distance between centers=3r
⇒ π 2 + ( c − d ) 2 = 9 r 2
Slope of radicle axis of circles=slope of tangent at (a,sin(a))
⇒ c o s ( a ) = d − c π
Shortest distance of tangent at (a,sin(a)) from center=radius of circle with that center
c o s 2 ( a ) + 1 ∣ 2 π c o s ( a ) + s e c ( a ) ( 2 π − a ) − a c o s ( a ) ∣ = 3 π s e c 2 ( a ) + 1
Its easy to find b=1/2 and a= 6 π and by symmetry, b=-1/2 also.