Surface area
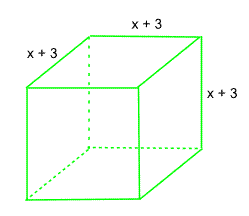
Find a polynomial expression for the surface area of the cube.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Area of a square: ( x + 3 ) ( x + 3 ) = ( x + 3 ) 2 Using the identity ( x + y ) 2 = x 2 + 2 x y + y 2 ⟹ = x 2 + 6 x + 9
There are 6 squares so: 6 × ( x 2 + 6 x + 9 ) ⟹ 6 x 2 + 3 6 x + 5 4
Each face of the cube is a square of length ( x + 3 )
The area of each square,
= ( x + 3 ) ( x + 3 )
= x ( x + 3 ) + 3 ( x + 3 )
= x 2 + 3 x + 3 x + 9
= x 2 + 6 x + 9
Now,
The cube has six such faces
The total surface area of the cube,
= 6 × The area of one face
= 6 ( x 2 + 6 x + 9 )
= 6 x 2 + 3 6 x + 5 4