Surface Area Enclosed by Projection

Calculus Level 5

Consider a unit-sphere centered at ( x , y , z ) = ( 0 , 0 , 0 ) (x,y,z) = (0,0,0) . In the same coordinate system, there is a circle with radius ( r = 1 2 (r = \frac{1}{2} ) which lies in the x y xy plane and is centered at ( 0 , 0 , 0 ) (0,0,0) .

If the circle is projected in the + z +z direction onto the surface of the sphere, the surface area enclosed by the resulting projection can be expressed as π ( a − b ) \pi (a - \sqrt{b}) .

Determine ( a + b ) (a+b)


The answer is 5.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Michael Mendrin
Aug 12, 2016

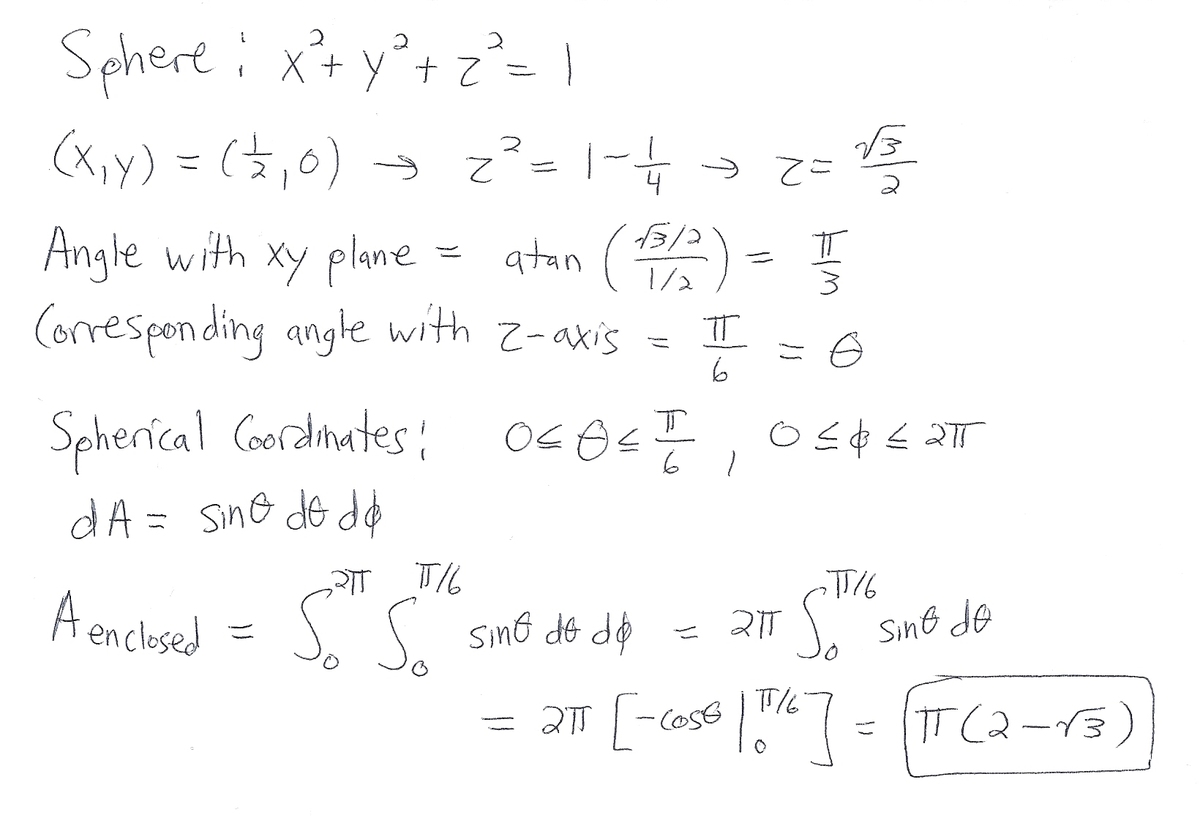
Given an unit sphere and any pair of parallel planes at a distance h < 2 h<2 , the surface area of the sphere between both the planes cutting it is equal to h h times half the area of the sphere. Here, the parallel planes would be spaced at

h = 1 − 1 − ( 1 2 ) 2 = 1 − 1 2 3 h = 1-\sqrt{1-{\left(\dfrac{1}{2}\right)}^{2} } = 1-\dfrac{1}{2} \sqrt{3}

so the area would be

1 2 4 π h = π ( 2 − 3 ) \dfrac{1}{2}4\pi h =\pi(2-\sqrt{3})

2 Helpful 1 Interesting 1 Brilliant 0 Confused
Steven Chase
Aug 10, 2016

2 Helpful 1 Interesting 1 Brilliant 0 Confused

@Steven Chase Sir i have realized my mistake.
I want to say sorry to you .
I will not repeat this again in future. I want to apologize not because for, after that you will clear my doubt,just because as a good student.
Please forgive me .


NJ STAR - 11 months ago

Thanks for the note. No worries, I'm not upset with you. I think you are a good guy. Just a few guidelines going forward:

1) If it takes me some time to reply, there is no need to send additional messages.
2) I might not reply to everything, since I have other things going on besides Brilliant

By the way, Krishna is worried since he thinks you have left the site. You might want to reassure him that you are still around.

Steven Chase - 11 months ago

Log in to reply

No worries mate; I figured out what his alt-account was and spoke to him.

Krishna Karthik - 11 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...