Surface area of a cuboid
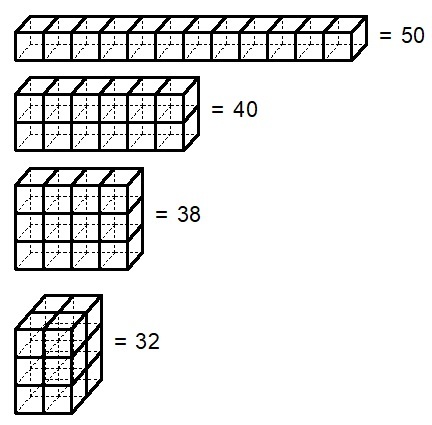
I want to arrange 12 unit cubes into a rectangular cuboid so that its surface area is maximized.
One way I can do it is by arranging each of these cubes from left to right. Can I increase the surface area further?
Note
: A rectangular cuboid is a three-dimensional solid with 6 rectangular faces.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
It's simple folding
Log in to reply
I agree. This has caused high rise building design issues since the wind shear at a 45 degree rotation will increase the structural requirements.
It is a tricky thing to do, but balancing them on edge as diamonds will expose more surface area.
Log in to reply
I was thinking the same thing. If they are connected by only their edge (as diamonds), the surface area would be even larger...
I agree. This has caused high rise building design issues since the wind shear at a 45 degree rotation ill increase the structural requirements.
The problem requires a rectangular cuboid
Moderator note:
This proof is done by showing every cuboid, and noting the surface area of the 1 by 1 by 12 cuboid is the largest. What it doesn't do is rigorously show this is the entire set of possible cuboids.
First cuboid: 1 by 1 by 12
We can split the 12 into two factors, leaving one of the dimensions as 1. As the factors of 12 are 2, 2, and 3, we could factor out 2, 3, 4, or 6. Factoring out a 2 leaves a 6 (and is equivalent to factoring out a 6) and factoring out a 3 leaves a 4 (and is equivalent to factoring out a 4).
Second cuboid: 1 by 2 by 6
Third cuboid: 1 by 3 by 4
Finally, we can split 12 into all three of its factors: 2, 2, 3. Since these are all prime this is the only way to split into three factors where none of the sides are 1.
Fourth cuboid: 2 by 2 by 3
Is this true in general? I.e., can you prove that the surface area of n unit cubes formed into a cuboid is always maximized when they are arranged in one row?
Log in to reply
My feeling says yes, but I have no proof. If we look at the number of faces that's out of sight, it seems that in a row that number is least. n-2 cubes have 2 faces covered and 2 cubes have 1 faces covered. This leads to an area of 6 n − 2 ( n − 2 ) − 2 = 4 n + 2 . But I in don't know for sure if there's not a configuration of n cubes which has less area loss.
I imagine you can prove it by starting with some arbitrary configuration, then show that moving the cubes more towards the n x 1 x 1 configuration implies that the surface area always increases.
I want to say "Yes". In the figure of result 40 above, It's still arranged from left to right, but 6 top unit cubes just connect to the under ones by their sides, It 's like this " / " or " \ " not like the second " | ".
This question seems contradictory, it states to get the maximum surface area, so doesn't the single separate unit cubes have more surface area than the long line depicted here?
Log in to reply
True, but the problem says that you must glue them together into a single cuboid.
Relevant wiki: Surface Area of a Cuboid
Imagine any rectangular cuboid constructed
1
2
of these unit cubes floating space.
The surface area of the cuboid can now be measured by how many faces of these unit cubes are visible.
This means that if we want to maximize the surface area, we want to maximize the number of the faces being visible.
However, some of the faces are hidden inside the cuboid and since we have a fixed number of cubes, and thus faces, it is equivalent to say that we want to minimize the number of faces hidden inside the cuboid.
However, to construct a rectangular cuboid out of these unit cubes, we must connect unit cubes by their faces, thus hiding some of the faces.
To construct a cuboid, we must start with a single unit cube and then connect the other cubes to it by faces.
This means that since we have
1
2
cubes, we have to hide at least
2
×
1
1
faces, because we have at least
1
1
face-to-face connections between the cubes.
However, in the example cuboid, we make exactly
1
1
face-to-face connections and thus hide
2
2
faces.
Hence, the example cuboid has the maximum possible area meaning that the answer is
No
.
How about a Triangle?
X X X
X X X X
X X X X X
Connect each one To Each corner to form a rectangle. That way all 72 faces can be counted.
For a given volume, the surface area of sphere is minimum. So, one could imagine that the arrangement in a straight line would have maximum surface area.
Set the solid in the picture as a fundamental cube. If we want the surface of this solid to be the maximum, we only choose to save the most 1×1 square surfaces. Every time we move a little cube somewhere else to make a new three dimensional solid, the fewest surfaces we delete must be 2 or 0. So, bsed on the solid in the picture 2, whatever move we make, we will only make the number of surfaces fewer or the same. As the consequence, the solid in the picture 2 has the maximum of surface area.
could we make it into a pyramid?
could we make it into a rectangular donut ?
Relevant wiki: Surface Area - Problem Solving
No calculations need to be done, as we can prove that this has the most surface area. To maximise the surface area, we want to minimise the number of joined faces, as each joining loses a surface area of 2 × ( 1 × 1 ) . By joining up each unit cube in a long line, this is meaning that the end cubes have 1 face joined and the rest have 2 faces joined. As this is the smallest possible way in this respect of connecting all the cubes together, it has the maximum surface area.