surface area of a solid
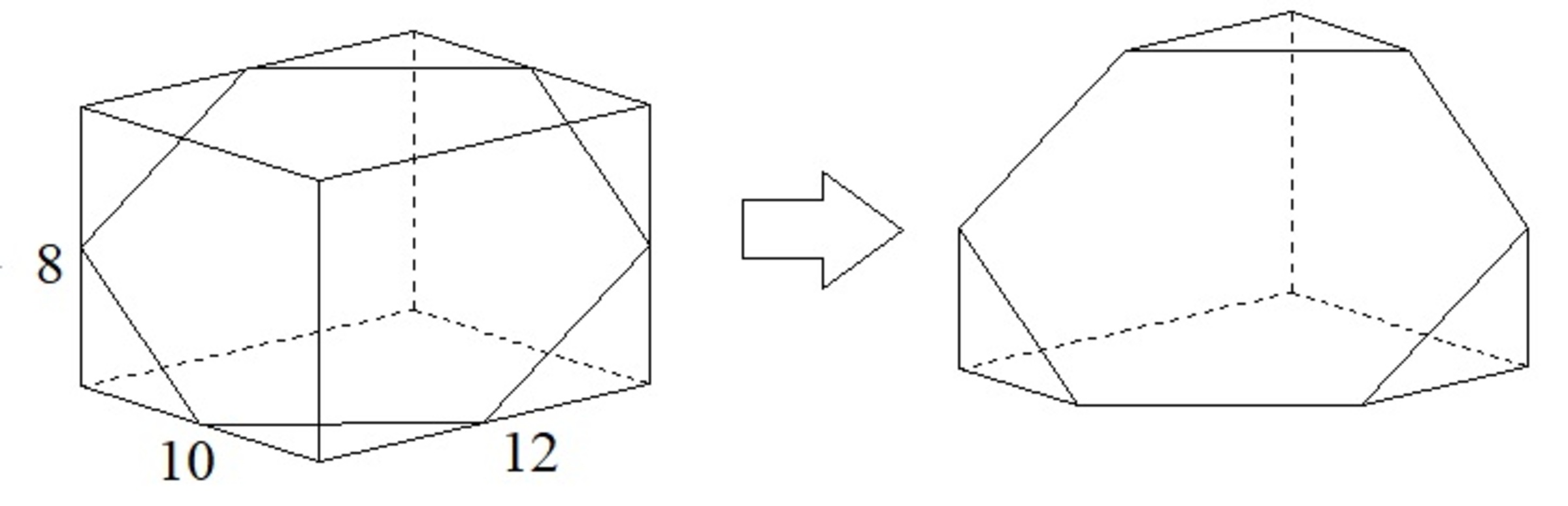 A cuboid measures
. A hexagonal plane cuts the cuboid into two equal solids. Find the surface area of one piece to the nearest integer.
A cuboid measures
. A hexagonal plane cuts the cuboid into two equal solids. Find the surface area of one piece to the nearest integer.
Note: The vertices of the hexagon lies on the midpoints of the edges of the cuboid.
The answer is 426.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
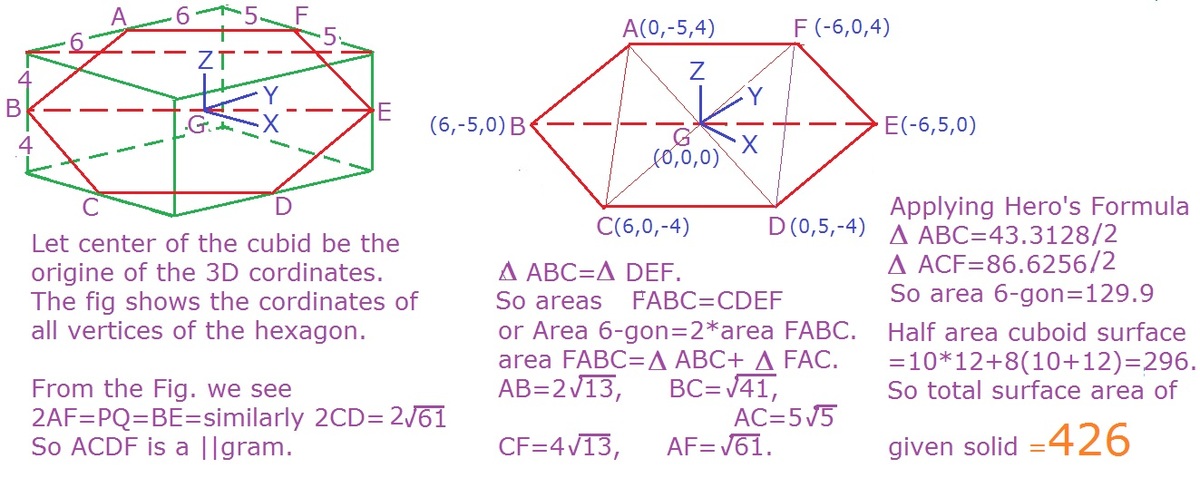
The surface area of the "half" cuboid is the area of the hexagon plus half the area of the original cuboid. To calculate the area of the hexagon, we first assign the center of the cuboid as the origin O of a vector space.
Then the vectors to the vertices of the hexagon are ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ A = − 5 i + 0 j + 4 k B = 0 i + 6 j + 4 k C = 5 i + 6 j + 0 k D = 5 i + 0 j − 4 k E = 0 i − 6 j − 4 k F = − 5 i − 6 j + 0 k
Consider the cross products, we note that A × B = B × C = C × D = D × E = E × F = F × A = − 2 4 i + 2 0 j − 3 0 k . ⟹ ∣ A × B ∣ = 2 4 2 + 2 0 2 + 3 0 2 = 2 4 6 9 . Note that 2 ∣ A × B ∣ = 4 6 9 is the area of the △ A O B . This means that the hexagon is made up of 6 triangle of equal area and the area of the hexagon is 6 4 6 9 . Therefore, the surface area of the "half" cuboid is 6 4 6 9 + 8 × 1 0 + 1 0 × 1 2 + 1 2 × 8 ≈ 4 2 6