Surface areas of solids
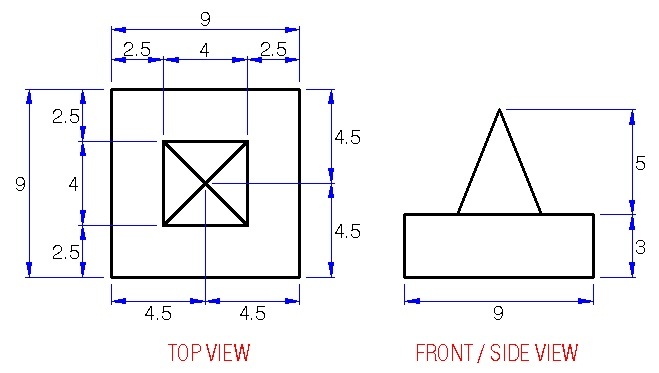 The above are the top, front and side views of a solid. Find the surface area of this solid. If your answer is of the form
, where
,
and
are positive integers with
being square-free, give your answer as
.
The above are the top, front and side views of a solid. Find the surface area of this solid. If your answer is of the form
, where
,
and
are positive integers with
being square-free, give your answer as
.
Note:
- All blue lines are dimension lines.
- All dimensions are unitless.
The answer is 291.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Surface Area - Problem Solving
The surface area of the prism is 2 [ ( 9 ) ( 9 ) + ( 3 ) ( 9 ) + ( 3 ) ( 9 ) ] = 2 7 0 . The area of the base of the pyramid is ( 4 ) ( 4 ) = 1 6 . The lateral area of the regular pyramid is 2 1 multiplied by the perimeter of the base multiplied by the slant height. The slant height can be computed by Pythagorean Theorem and it is 2 9 . Therefore, the lateral area of the regular pyramid is 2 1 ( 4 ) ( 4 ) ( 2 9 = 8 2 9 .
Thus, the surface area of the solid is 2 7 0 + 8 2 9 − 1 6 = 2 5 4 + 8 2 9 .
Finally,
a + b + c = 2 5 4 + 8 + 2 9 = 2 9 1