Surface areas of solids
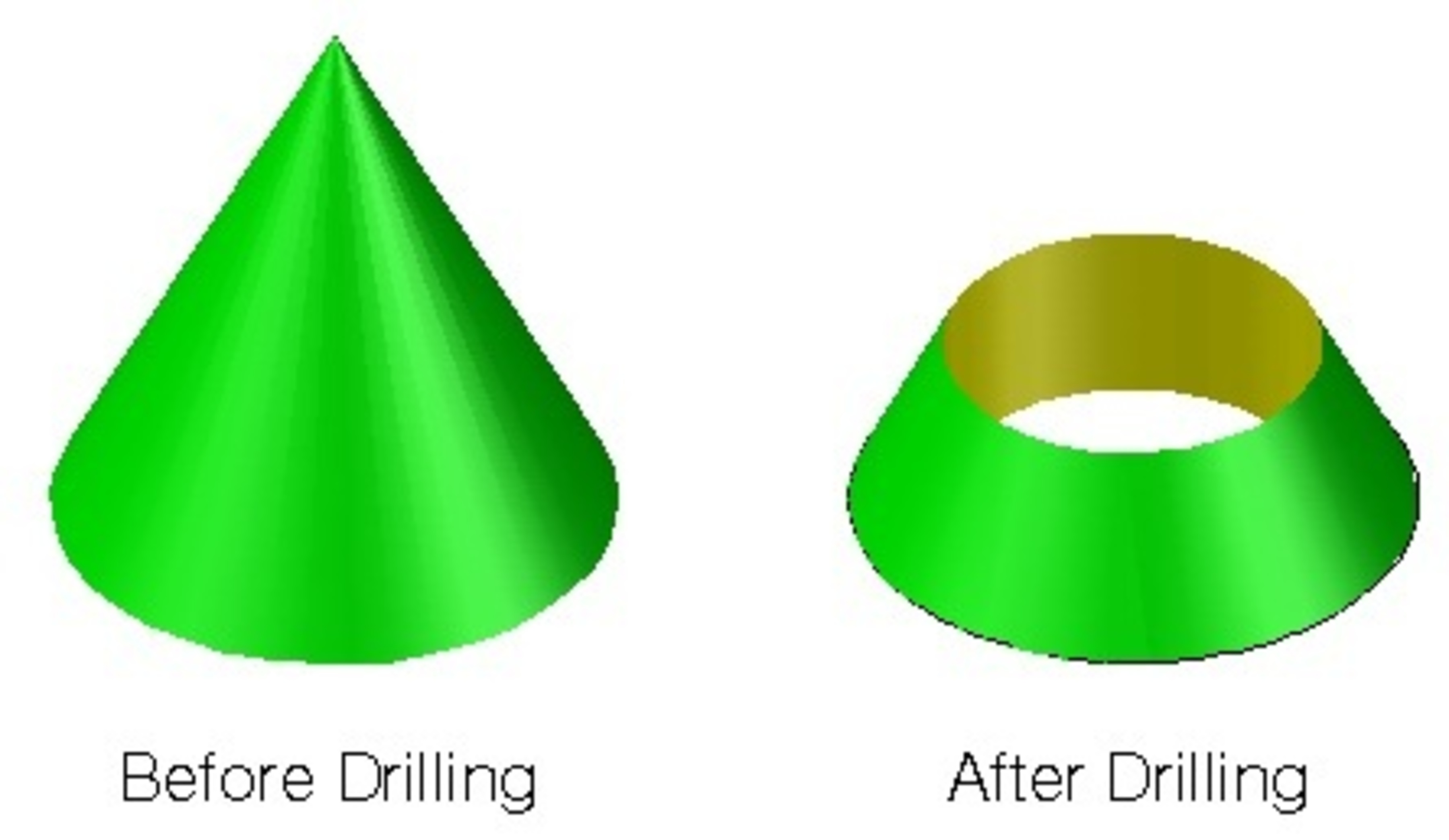 The radius and height of a right circular cone are 6 cm and 12 cm, respectively. A right circular cylinder with the maximum volume is to be drilled through the base. Find the surface area of the resulting solid in
.
The radius and height of a right circular cone are 6 cm and 12 cm, respectively. A right circular cylinder with the maximum volume is to be drilled through the base. Find the surface area of the resulting solid in
.
If the surface area is in the form ), where are integers with square-free, give your answer as .
The answer is 82.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
let y be the height and r be the radius
By similar similar triangles, we have
6 − r y = 6 1 2 = 2 ⟹ y = 1 2 − 2 r
Find the volume of the right circular cylinder.
V = π r 2 y = π r 2 ( 1 2 − 2 r )
Differenciate with respect to r applying the product rule.
d r d V = π [ r 2 ( − 2 ) + ( 1 2 − 2 r ) ( 2 r ) ] = π ( − 2 r 2 + 2 4 r − 4 r 2 ) = π ( − 6 r 2 + 2 4 r )
For maximum volume, d r d V = 0 .
π ( − 6 r 2 + 2 4 r ) = 0 ⟹ 6 r 2 = 2 4 r ⟹ r = 4
It follows that,
y = 4
Solving for the surface area of the resulting solid:
The surface area of the resulting solid is equal to the lateral area of a frustum of a cone plus lateral area of the right circular cylinder plus area of the base. The lateral area of the frustum of a cone is 2 1 multiplied by the sum of the circumference of the two bases multiplied by the slant height, that is 2 1 ( 8 π + 1 2 π ) ( 2 0 ) = 1 0 π 2 0 . The lateral area of the cylinder is circumference of the base multiplied by the height, that is 8 π ( 4 ) = 3 2 π . The area of the base is area of the big circle minus area of the small circle, that is 4 π ( 1 2 2 − 8 2 ) = 2 0 π .
Summing up the three areas, we get
π ( 1 0 2 0 + 5 2 )
Finally,
a + b + c = 1 0 + 2 0 + 5 2 = 8 2