Swapped Digits

Algebra Level 3

Let the capital letters $A$ and $B$ be single digits that form a two-digit number when concatenated as shown below.

$AB × (AB+1)\% = BA$

Add all the possible non-zero integer values of $A$ and $B$ that satisfy the equation.

NOTE: For clarification, $AB$ and $AB+1$ are consecutive numbers.

Try Part 2

The answer is 30.

3 solutions

Mahdi Raza
May 21, 2020

Brute force Coding:

a = 0
b = 0
total = 0

for a in range(10):
    for b in range(10):
        if ((10*a + b) * (10*a+b+1)/100 == 10*b + a):
            total = total + a + b

print(total)

Well, since $AB$ and $AB + 1$ are consecutive two digit integers, you can just do the for loop once:

total = 0

for integer in range(10, 99 + 1):
    # AB = integer
    # BA = 10 * (integer mod 10) + (integer quotient 10)
    right_hand_side = 10 *( integer % 10 ) + (integer // 10)

    if integer * (integer + 1)/100 == right_hand_side: total += (integer // 10) + (integer % 10)

print(total)
# Output: 30

Pi Han Goh - 1 year ago

Looks good. Thanks for sharing!

Mahdi Raza - 1 year ago

Aaghaz Mahajan
May 22, 2020

If we denote $AB\$ by $n$ then, we observe that $n\cdot\left(n+1\right)$ should be divisible by $100$ . Hence, we only need to check those values of $n$ for which either $n$ OR $n+1$ are multiples of $25$ . Simply checking leads us to the values of $n$ being $75$ and $99$

Kaizen Cyrus
May 21, 2020

Let $A$ be $x$ and $B$ be $y$ . In the left side of the equation shown in the question, the expression can be interpreted as this:

$(10x+y)×\frac{10x+y+1}{100}$

And as such, the right expression can be written as $10y+x$ . With these information we can plot a graph of the equation. Since we're looking for digits as value, we only look at the values $1$ to $9$ of $x$ and $y$ . Also, we're looking for the points on the parabola that are integers with their coordinates.

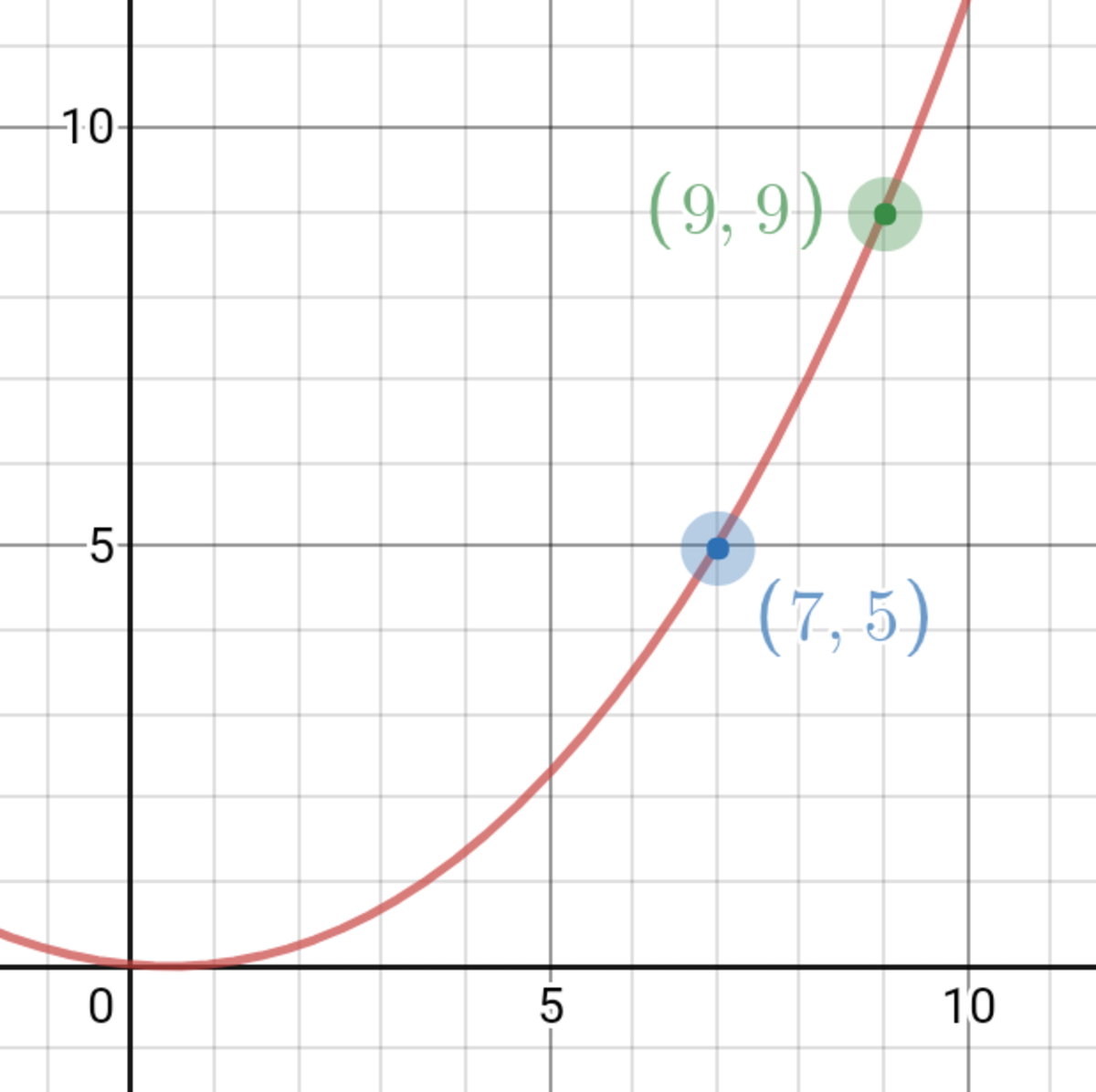
In the graph , the parabola crosses integer pairs: $(7,5)$ , $(9,9)$ . Let's check by substituting.

$75×76\% = 57$ $99×100\% = 99$

We add all the values and we get $\boxed{30}$ .

I missed $99$ and lost the chance to post my solution. If you don't mind, I'm posting it here.

Let $n=\overline {AB}$ , a two digit number with digits $A$ and $B$ . Then $\overline {BA}$ is also a two digit number.

So $1000\leq n(n+1)=n^2+n\leq 9999\implies 31<n\leq 99$ , and $n(n+1)$ must be divisible by $100$ (since $\overline {BA}$ is an integer).

Since both of two consecutive numbers can't be even, one must be a multiple of $4$ . Since both of two consecutive numbers can not be a multiple of $5$ , one of them must be a multiple of $25$ .

Only two pairs, namely $(75,76)$ and $(99,100)$ satisfy the given conditions. So the required sum is $7+5+9+9=\boxed {30}$ .

A Former Brilliant Member - 1 year ago

Swapped Digits

The answer is 30.

3 solutions

Brute force Coding:

0 pending reports