Swapping In And Swapping Out

Probability Level 4

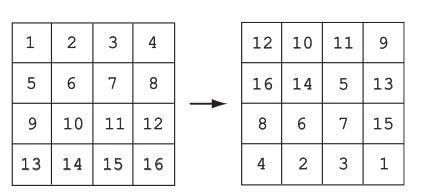
How many distinct matrices can be formed by swapping rows and columns of a 4 × 4 4 \times 4 matrix with all distinct elements?

Hint/Bonus : Try proving that swapping columns or rows cannot transform the left matrix into the right matrix above.


The answer is 576.

View wiki
Agnishom Chattopadhyay by Agnishom Chattopadhyay , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Otto Bretscher
Feb 29, 2016

We can permute the rows and the columns independently, forming a total of ( 4 ! ) 2 = 576 (4!)^2=\boxed{576} matrices

Bonus: The first matrix in singular (first row + third row = twice the second row), while the second one is invertible (with determinant 1600).

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Easier for bonus: 1,2,5,6 should remain corners of a rectangle.

Ivan Koswara - 5 years, 3 months ago

Log in to reply

Good observation! Even easier: 1 and 5 remain in the same column ;)

Otto Bretscher - 5 years, 3 months ago

It is odd that the Hint is described as a Bonus, since it is integral to getting the answer in the first place.

The elements of any row of the matrix always stay together in the same row, and the elements of any column of the matrix always stay together in the same column. Thus deciding on a permutation of rows and a permutation of columns determines the resulting matrix precisely, and so all we have to do is count the number of possible permutations of columns and rows.

The second matrix in the example cannot be obtained from the first, since it violates the "preservation of row/column content" principle.

Mark Hennings - 5 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...