Swapping Ints
Computer Science
Level
5
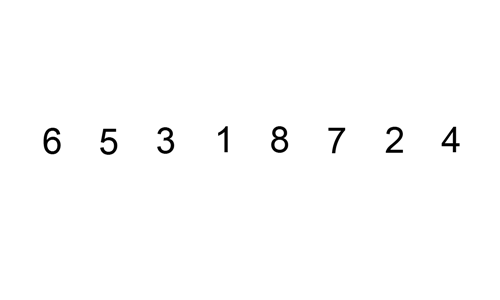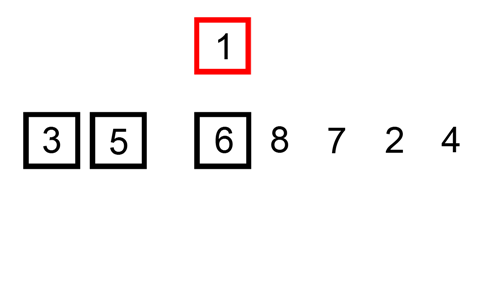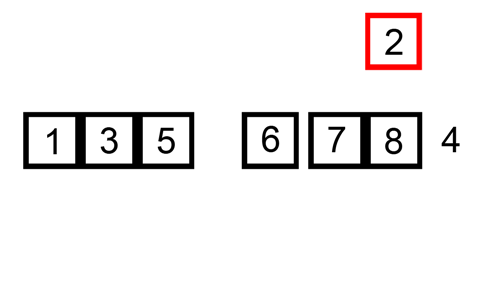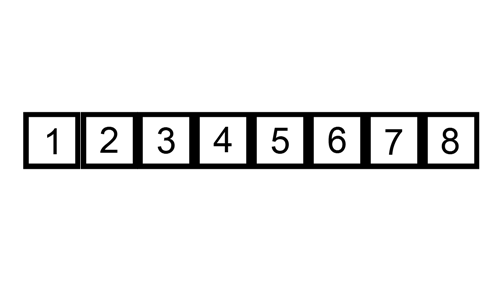 What is the minimum number of swaps operations a standard insertion sort implementation performs on the following
list of numbers
?
What is the minimum number of swaps operations a standard insertion sort implementation performs on the following
list of numbers
?
The answer is 6240542.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The problem is basically asking for the list inversion. That is the pair of elements ( i , j ) in A [ 0 . . . . . . n ] such that i < j and A [ i ] > A [ j ] .
Just like the maximum sub-array problem we use a divide and conquer approach, An inversion i , j can occur in the left half, right half and i on the left half and j on the right half. We implement a modified merge-sort algorithm which in addition to sorting also counts the number of inversion. First lets implement a
mergesubroutine to count the number of inversion between the left and right sorted sub-arrays. For every element in the left sub-array(left[i]) we look for an element in the right sub-arrays(right[i]) that is strictly smaller than left[i].With the merge procedure at hand we can write a divide and conquer algorithm Base case: return 0 if the number of elements is equal to one else: recur on the left and right half
The algorithm runs in O ( n l o g n ) .