Swirling In
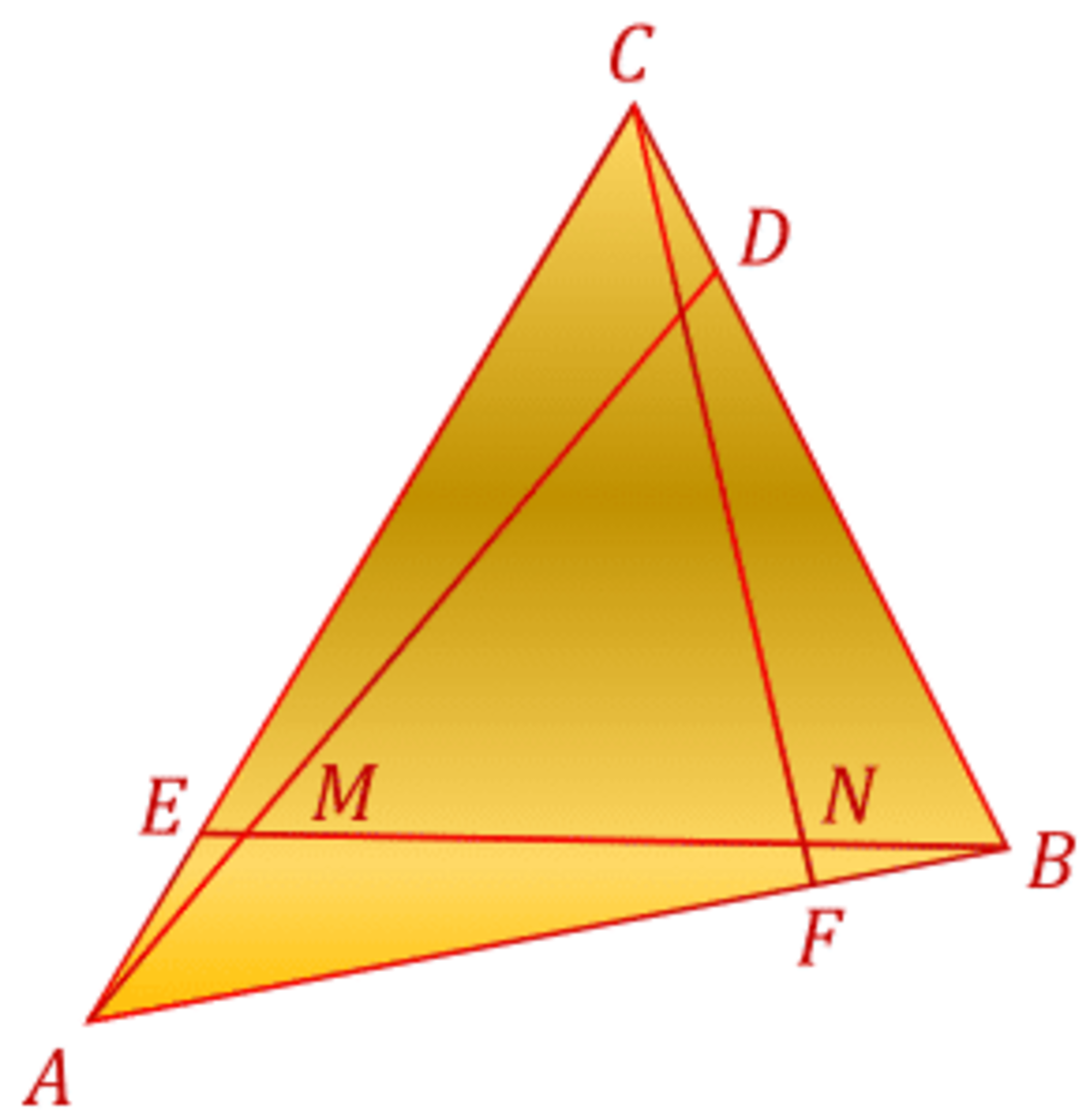
In a triangle , we are given the ratios .
If the value of can be expressed as , where and are coprime positive integers, find .
Note: The drawing in not to scale.
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
It is generally true that if A F F B = D B C D = E C A E = n ,then N B M N = n − 1 .
To prove this, I will work with a right triangle. The result will hold true for any triangle derived from it by a linear transformation (that is for any triangle) since linear transformation does not affect ratios of lengths on the same straight line.
Assume A C = A B = n + 1 . Then equations of the internal lines will be:
y = n x
y = 1 − n + 1 1 x
y = n + 1 − n n + 1 x
The x -coordinate of M will come from the intersection of the first two and it will be
x 1 = n 2 + n + 1 n + 1
The x -coordinate of N will come from the intersection of the last two lines and it will be
x 2 = n 2 + n + 1 n 2 ( n + 1 )
The difference between them will need to be divided by the difference between x 2 and n + 1 .
n 2 + n + 1 ( n + 1 ) ( n 2 + n + 1 ) − n 2 ( n + 1 ) n 2 + n + 1 ( n 2 − 1 ) ( n + 1 ) = n 2 + 2 n + 1 ( n − 1 ) ( n + 1 ) 2 = n − 1
The ratio has to be the same for the y -coordinates and for the lengths themselves, as they all refer to the same straight line and are non-zero.
For n = 1 7 the result is 1 6 = 1 1 6 , so the answer is 1 6 + 1 = 1 7 .