Switch
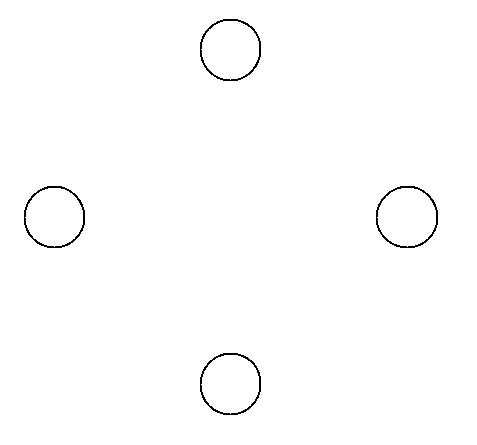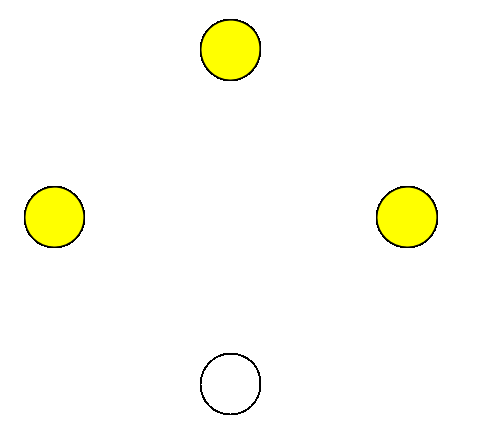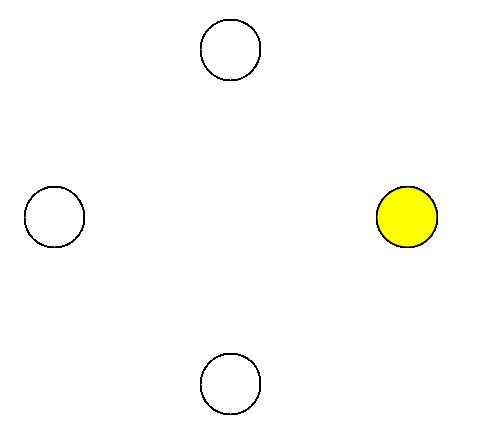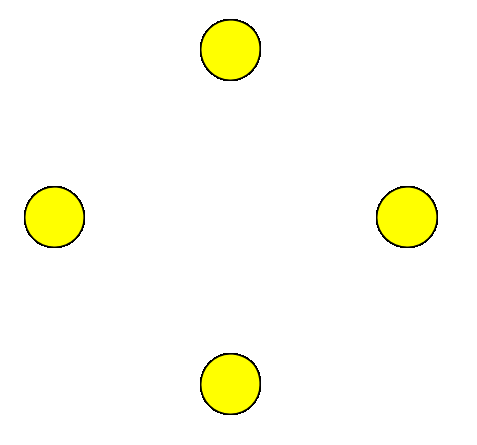
There is a circle of light bulbs with a switch next to each of them. Each switch can be flipped between two positions, thereby toggling the on/off states of three lights: its own and the two lights adjacent to it. Initially, all the lights are off.
Let the minimum number of flips needed to turn on all the and light bulbs be and , respectively. Then what is the value of ?
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Information Compression
General solution:
Let us have n light bulbs labeled a 1 , a 2 , ⋯ , a n and n switches labeled b 1 , b 2 , ⋯ , b n .
If n ≤ 3 clearly the minimum number of flicks is 1 since any flick causes every light bulb to turn on.
Now, if n > 3 is divisible by 3 clearly the minimum number of flicks needed is 3 n because flicking every third switch turns every light bulb on.
However, if n > 3 is not divisible by 3 the minimum number of flicks needed is n .
Proof:
If we flick a switch, for instance b i , lamps a i − 1 , a i and a i + 1 turn on.
Now if we flick b i + 1 by induction we must also flick b i + 2 and hence every switch must be flicked resulting the minimum number of flicks to be n . Also, by symmetry, flicking b i − 1 gives the same result.
If we flick b i + 2 we must also flick b i + 1 because lamp a i + 1 is on and flicking any switch again makes no sense, since we already have flicked it. This gives the same result.
Now we are forced to flick b i + 3 since it is the only possible way to try to turn lamp a i + 2 on without flicking every switch.
We continue like this, flicking every third switch, but this results in us flicking every switch because n is not divisible by 3 .
Thus, the minimum number of flicks in this case is n . □
Answer to the problem:
Using the general solution we find that a = 4 , b = 1 3 ⇒ a + b = 1 7 .