Switching numerator and denominator
a 5 = b + c , b 1 0 = c + a , c 1 3 = a + b .
Let a , b , c be positive real numbers satisfying the equations above.
What is a b c ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
5 = a b + a c 1 0 = a b + b c 1 3 = a c + b c Adding all three equations yields 2 8 = 2 ( a b + b c + a c ) Now, we can plug in each of the first equations into this newly derived equation to find that b c = 9 , a c = 4 , a b = 1 .
Therefore, a = 3 2 , b = 2 3 , c = 6 ,
which multiply to ( 3 2 ) ( 2 3 ) ( 6 ) = 6 .
Moderator note:
Good approach. The substitution of A = a b , B = b c , C = c a was hard to see.
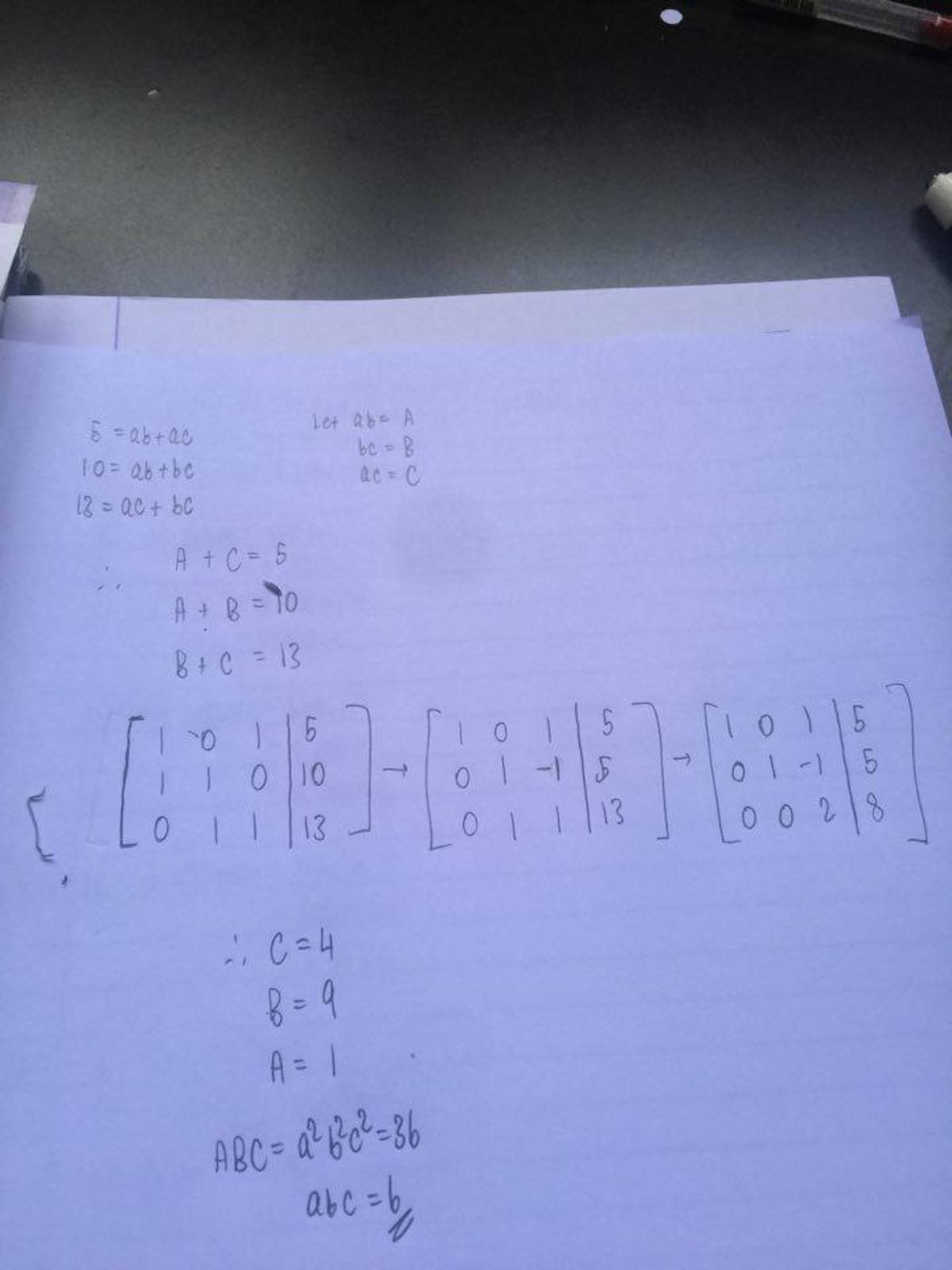
The three equations are equivalent to
a b + a c = 5
b c + a b = 1 0
a c + b c = 1 3
Therefore, 2 = 5 + 1 0 − 1 3 = ( a b + a c ) + ( b c + a b ) − ( b c + a c ) = 2 a b ⟹ a b = 1
Similarly, we can get b c = 9 , a c = 4 .
Thus, a b . b c . a c = ( a b c ) 2 = 3 6 ⟹ a b c = 6