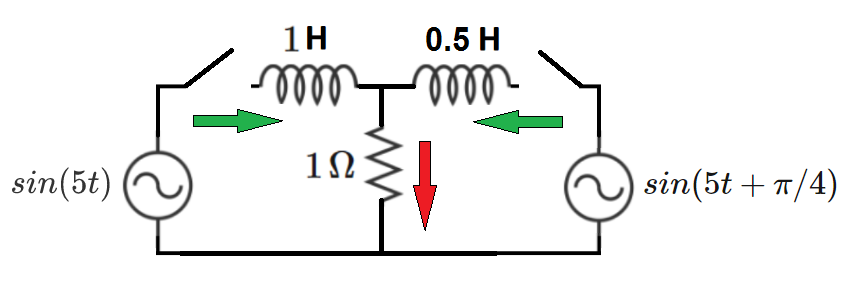
Switching Onto a Fault

Electricity and Magnetism Level 4

Both switches close at time $t =0$ . Prior to switch closing, both inductors are de-energized. What is the maximum instantaneous current which flows through the resistor? If this value is $I_m$ , give your answer as $\lfloor 1000 \, I_m \rfloor$ .

The answer is 548.

1 solution

Karan Chatrath
May 13, 2019

Consider the given circuit. The governing equations of this circuit can be determined using Kirchoff's current and voltage laws. The resulting system of paired differential equations turns out to be:

$\frac{di_1}{dt} = -i_1 - i_2 +\sin(5t)$

$\frac{di_2}{dt} = -2(i_1 + i_2) +2\sin(5t+\frac{\pi}{4})$

Here, $i_1$ is the current through the 1H inductor while $i_2$ is the current through the 0.5H inductor. The current through the resistor is: $i = i_1 + i_2$

This system of ODEs can be solved analytically. However, I have chosen to solve them numerically. The currents $i_1$ and $i_2$ are both zero at $t = 0$ .

The solution for the current through the resistor looks as such: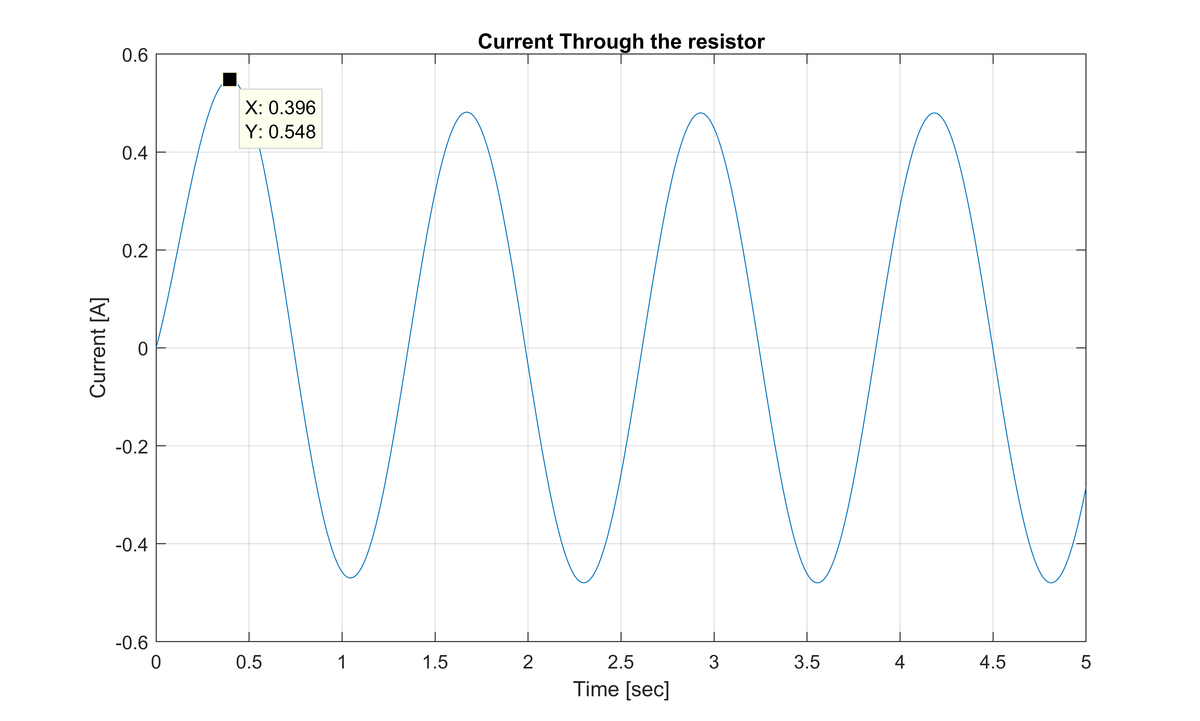

From here, it can be concluded that the required answer is 548

On an unrelated note, I recently attempted one of your problems on finding the minimum distance between a circle and a helix. I got the incorrect answer. It would be very helpful if you could post a solution to that problem, so that I can learn from my mistake.

Karan Chatrath - 2 years ago

Thanks for the solution. On the other problem, what did you get for a minimum? If it's less than 0.02, I might have to go back and look again.

Steven Chase - 2 years ago

0.502. I solved it as such: I computed the Euclidean distance between two arbitary points. I then calculated the partial derivatives with respect to the independent variables and equated them to zero. I attempted to solve that system of nonlinear equations on a computer.
This was my first attempt. I then 3D plotted both curves and tried to estimate the shortest distance from the plot (a cheat code of sorts), and I entered my answer close to 0.02 but was off by a decimal place.

Karan Chatrath - 2 years ago

Yeah, I started down that path and then got afraid of local minima. So I resorted to brute search over the parameter space instead.

Steven Chase - 2 years ago

I hadn't thought of multiple local optimal points. Do you suggest that I attempt solving the system of equations with different starting (initial) points? Many numerical solvers require an initial guess.

Karan Chatrath - 2 years ago

Actually, multi-start numerical solving would still be tedious. I took your suggestion and attempted to find the global optimum by brute force. The value I arrive at, by varying the independent variables between -20 and 20 with a step of 0.01, is 0.0199778. It is very close to the answer. Thank you for the suggestion

Karan Chatrath - 2 years ago

Ok, that's a relief. Yeah, I think formal methods are confounded by multiple local optima. Random initialization would help, but even then, there would be some uncertainty. With brute force, we know for certain that we have the right answer.

Steven Chase - 2 years ago

Switching Onto a Fault

The answer is 548.

1 solution

0 pending reports