Symmedian Point
In △ A B C , G is the centroid and K is the Symmedian point. If A B = 1 3 , B C = 7 , and G K is parallel to A B , what is A C ?
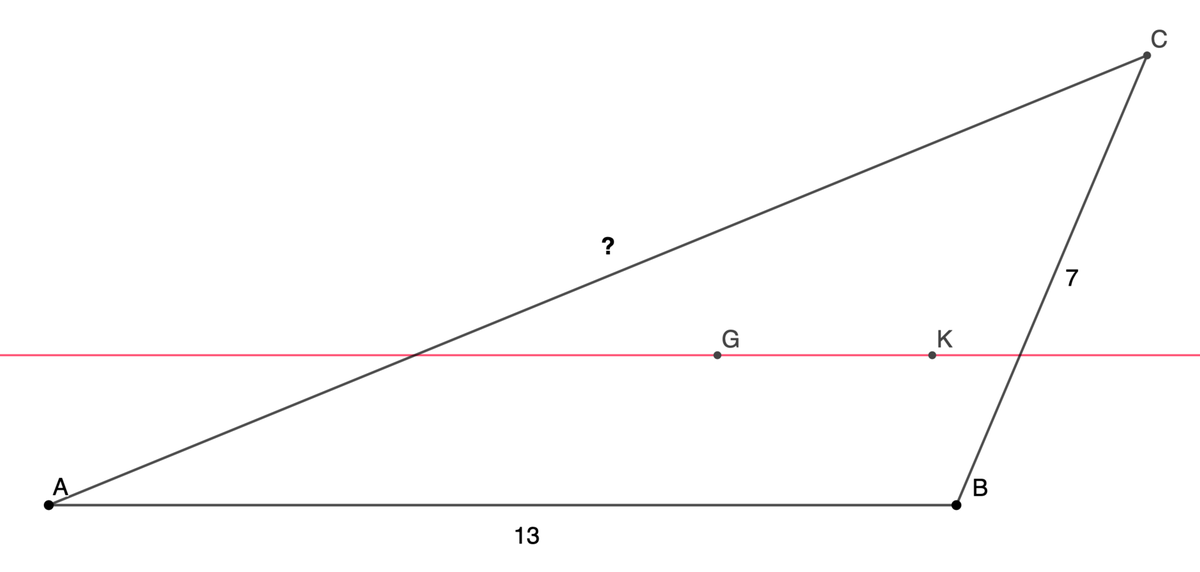
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You are brilliant @Mark Hennings
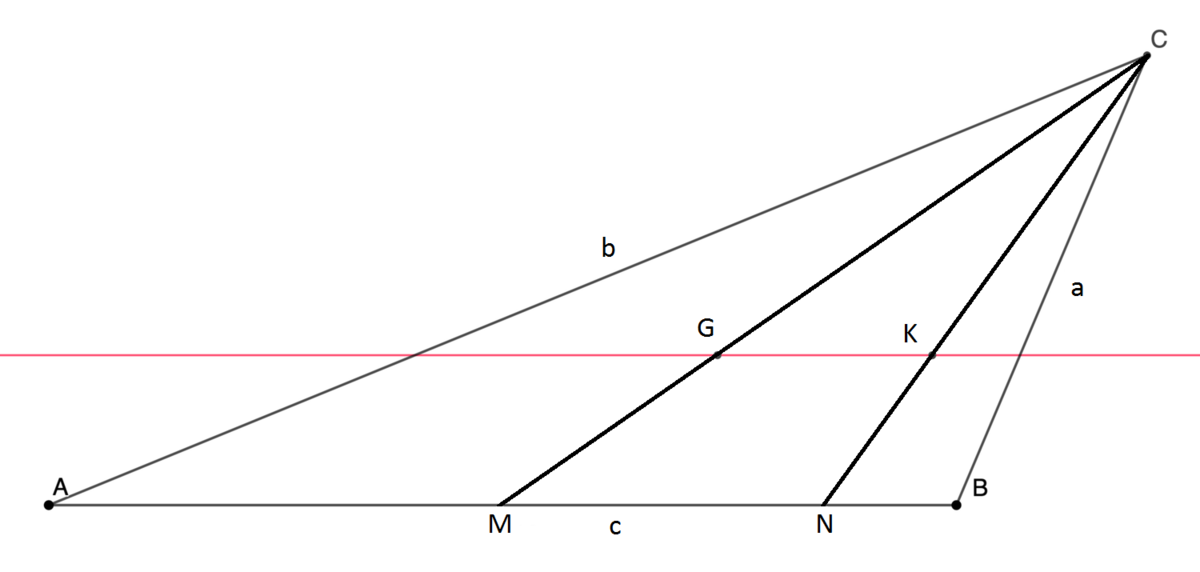 Let
C
K
→
∩
A
B
=
N
and
C
G
→
∩
A
B
=
M
.
Since
G
K
∣
∣
M
N
the Basic Proportionality Theorem (or Thales' Theorem) gives:
G
M
C
G
=
K
N
C
K
The centroid splits the median in ratio
2
:
1
from the vertex and the symmedian point splits the symmedian from vertex
C
in ratio
c
2
a
2
+
b
2
. Substituting these values in the result form Thales' Theorem and rearranging gives:
2
c
2
=
a
2
+
b
2
⇒
b
=
2
c
2
−
a
2
=
2
.
1
3
2
−
7
2
=
1
7
Let
C
K
→
∩
A
B
=
N
and
C
G
→
∩
A
B
=
M
.
Since
G
K
∣
∣
M
N
the Basic Proportionality Theorem (or Thales' Theorem) gives:
G
M
C
G
=
K
N
C
K
The centroid splits the median in ratio
2
:
1
from the vertex and the symmedian point splits the symmedian from vertex
C
in ratio
c
2
a
2
+
b
2
. Substituting these values in the result form Thales' Theorem and rearranging gives:
2
c
2
=
a
2
+
b
2
⇒
b
=
2
c
2
−
a
2
=
2
.
1
3
2
−
7
2
=
1
7
Very nice solution! Thank you for sharing it.
The centroid G and the symmedian point K have barycentric coordinates 1 : 1 : 1 and a 2 : b 2 : c 2 respectively, and so the line G K has barycentric equation ( b 2 − c 2 ) x + ( c 2 − a 2 ) y + ( a 2 − b 2 ) z = 0 while the line A B has barycentric equation z = 0 These two lines meet at the point with baycentric coordinates a 2 − c 2 : b 2 − c 2 : 0 . Since A B and G K are parallel, this must be the point at infinity, and hence its coordinates must sum to 0 . Thus we deduce that a 2 + b 2 = 2 c 2 . With a = 7 and c = 1 3 , we deduce that b = 1 7 .