Symmedian Simplicity
 The triangle
A
B
C
is formed with points
A
and
B
being diametrically opposite points on a unit circle, and
C
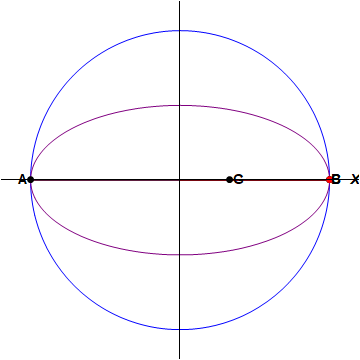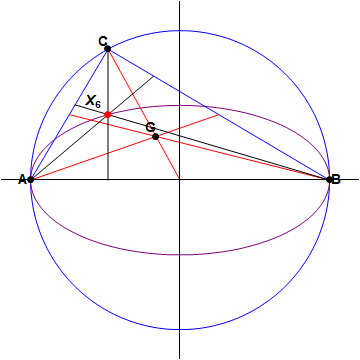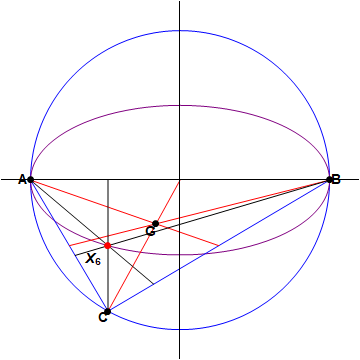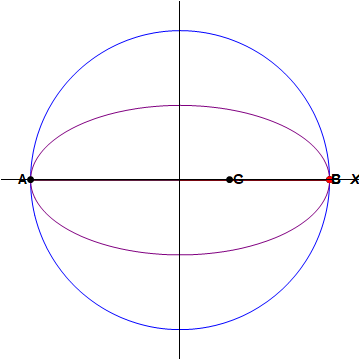
being another point on that circle. The locus of the Symmedian point
X
6
of the triangle
A
B
C
, as
C
varies, is an elegant smooth curve. The area of the region enclosed by the locus is of the form
b
a
π
where
a
,
b
,
c
are coprime positive integers. Find the value of
a
+
b
.
The triangle
A
B
C
is formed with points
A
and
B
being diametrically opposite points on a unit circle, and
C
being another point on that circle. The locus of the Symmedian point
X
6
of the triangle
A
B
C
, as
C
varies, is an elegant smooth curve. The area of the region enclosed by the locus is of the form
b
a
π
where
a
,
b
,
c
are coprime positive integers. Find the value of
a
+
b
.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The Lemoine point of a right angled triangle is the midpoint of its altitude corresponding to the right angle.
Proof:-
Let A C B be a right triangle with ∠ C = 9 0 ∘ . Let O be the midpoint of AB and F the foot of ⊥ from C on AB. We have:
∠ A C O = ∠ A = π / 2 − ∠ B = ∠ B C F
⇒ C F and C O are isogonals.
Let M be the midpoint of C F and M A the midpoint of B C . We have:
Δ A C B ∼ Δ A F C
⇒ ∠ C A M A = ∠ F A M
⇒ A M A and A M are isogonals.
∴ M is the isogonal conjugate of the centroid G , so, M ≡ X 6 □
Let f ( x ) denote the locus of the point C as x ≡ F varies over path ρ = [ A − B − A ] .
The required area = ∫ ρ ∣ 2 f ( x ) ∣ d x = 2 ∫ ρ ∣ f ( x ) ∣ d x = 2 Area of Circle(r=1) = 2 π .
The Symmmedian point X 6 is the isogonal conjugate of the centroid G of the triangle. Suppose that ∠ B A C = θ , so that A , B , C have coordinates A ( − 1 , 0 ) B ( 1 , 0 ) C ( cos 2 θ , sin 2 θ )
If C F is the symmedian of A B C corresponding to the median C O then, since ∠ O C A = θ , we deduce that ∠ F C B = θ , which implies that triangle C F B is right-angled, with ∠ C F B = 9 0 ∘ .
Now let A D be the symmedian corresponding to the median A M A , and let ∠ M A A C = α , so that tan α = 2 cos θ sin θ = 2 1 tan θ . But then ∠ D A B = α , and hence X 6 F = A F tan α = ( cos 2 θ + 1 ) × 2 1 tan θ = sin θ cos θ = 2 1 sin 2 θ which means that X 6 has coordinates ( cos 2 θ , 2 1 sin 2 θ ) , and hence the locus of X 6 is the ellipse x 2 + 4 y 2 = 1 which has semimajor axis a = 1 and semiminor axis b = 2 1 . Thus the area of the enclosed region is π a b = 2 1 π which makes the answer 1 + 2 = 3 .