Symmetric Sextic

Due to symmetry of the regular pentagon, we can expect the sextic polynomial $f(x)$ to be an even function with one of the vertices or turning points at $x=0$ and the other four at $x=\pm \cos \frac {3\pi}{10}$ and $x = \pm \cos \frac \pi{10}$ . Since turning points occur when $f'(x)=0$ , we have:

$\begin{aligned} f'(x) & = x \left(x+\cos \frac {3\pi}{10} \right) \left(x-\cos \frac {3\pi}{10} \right) \left(x+\cos \frac \pi{10} \right) \left(x-\cos \frac \pi{10} \right) \\ & = x \left(x^2-\cos^2 \frac {3\pi}{10} \right) \left(x^2-\cos^2 \frac \pi{10} \right) \\ & = x \left(x^4- \left(\cos^2 \frac {3\pi}{10} + \cos^2 \frac \pi{10} \right)x^2 + \cos^2 \frac {3\pi}{10} \cos^2 \frac \pi{10} \right) \\ & = x^5 - \frac 54 x^3 + \frac 5{16}x & \small \blue{\text{Integrate both sides w.r.t. }x} \\ \implies f(x) & = k \left(\frac {x^6}6 - \frac 5{16}x^4 + \frac 5{32}x^2 \right) + C & \small \blue{\text{where }k \text{ and }C \text{ are constants.}} +\end{aligned}$

Let $C=0$ . Then for positive first coefficienet $\frac k6$ , $(0,0)$ is the global minimum of $f(x)$ . The other turning points are $\left(\pm \cos \frac {3\pi}{10}, 1+\sin \frac {3\pi}{10}\right)$ and $\left(\pm \cos \frac \pi{10}, 1- \sin \frac \pi{10} \right)$ . Therefore,

$\begin{cases} k \left(\frac 16 \cos^6 \frac {3\pi}{10} - \frac 5{16} \cos^4 \frac {3\pi}{10} + \frac 5{32} \cos^2 \frac {3\pi}{10}\right) = 1+\sin \frac {3\pi}{10} & \implies k = 76.8 \\ k \left(\frac 16 \cos^6 \frac {\pi}{10} - \frac 5{16} \cos^4 \frac {\pi}{10} + \frac 5{32} \cos^2 \frac {\pi}{10}\right) = 1-\sin \frac {\pi}{10} & \implies k = 76.8 \end{cases}$

Therefore the leading coefficient is $\dfrac k6 = \dfrac {76.8}6 = 12.8 = \dfrac {64}5$ , $\implies a+b = 64+5 = \boxed{69}$ .

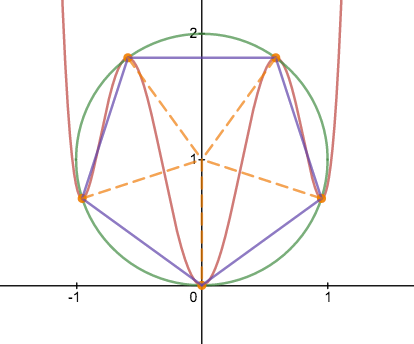
My solution:

The sextic has turning points at each vertex. Hence there must be a double root at the origin.
Also, the sextic must be an even function, i.e. symmetrical about the $y-$ axis.
Based on the above, the sextic must be of the form $\displaystyle y=kx^2 (x^4+ax^2 +b)$ where $k$ is the leading coefficient.

Differentiating gives $\frac {dy}{dx}=6kx (x^4+\tfrac 23 ax^2 +\tfrac 13 b) =0$ at turning points.

Now consider the regular pentagon standing inverted with apex at the origin.
The non-origin vertices are $( ± \sin\theta, 1-\cos\theta), (\pm\sin\frac {\theta}2, 1+\cos\frac{\theta}2)$ ,
where $\theta=\frac {2\pi}{5}$ , the central angle of the pentagon.

It can be shown that $\cos\theta = \frac {\sqrt{5}-1}4$ and $\cos\frac{\theta}2 = \frac {\sqrt{5}+1}4$ .

This gives $x^4+\tfrac 23 ax^2 +\tfrac 13 b =0 =(x^2-\sin^2 \theta )(x^2 - \sin^2 \frac{\theta}2) = \left(x^2 - \frac {5+\sqrt{5}}8 \right) \left( x^2 -\frac {5-\sqrt{5}}8 \right)$ .

Sum of roots $= \frac 54 = \frac 23 a \Rightarrow a = \frac {15}8$ . Product of roots $= \frac 5{16} = \frac 13b \Rightarrow b=\frac {15}{16}$ .

Hence the sextic is $\displaystyle y=kx^2 (x^4+\tfrac {15}8x² +\tfrac {15}{16})$ .

Substitute $x²=\sin^2 \theta =\frac {5+\sqrt{5}}8$ and $y=1-\cos\theta =\frac {5-\sqrt{5}}4$ .

After some nifty surd manipulation, we arrive at $\large k=\color{#D61F06}\frac {64}5$ .

This can be confirmed by substituting $x²=\sin^2 \frac\theta 2 =\frac {5-\sqrt{5}}8$ and $y=1+\cos\frac\theta 2 =\frac {5+\sqrt{5}}4$ .

The answer required is $64 + 5 = \color{#D61F06}69$ .