Symmetry Destroyed 2

If the intersection of $EF$ and $AC$ is $M$ , then $EM\mid\mid DA$ . Since $DE=EC, AM=MC$ . So $EM$ is a median of $\triangle ACE$ . Therefore the two areas are equal.

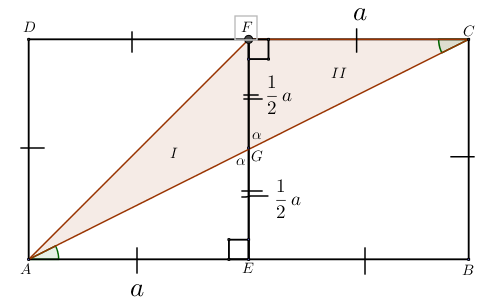
$AGE$ triangle is congruent with $FGC$ triangle. So $FG = G$ E. The area of an $AFG$ triangle is $\frac { 1 }{ 2 } \times FG \times AE$ and the area of the $FGC$ triangle is $\frac { 1 }{ 2 } \times FC \times FG$ where $FC = AE$ . So the area of triangle $AGF = FGC$ .

In this case the intersection point between $\overline{AC}$ and $\overline{EF}$ is right in the middle of the rectangle. Let's call it as O. The $\triangle AOE$ and the $\triangle EOC$ have the same base $\overline{EO}$ and same height $\overline{DE}= \overline{EC}$ . So, they have the same area. In this case O is the midpoint of $\overline{AC}$ but its position don't matters at all. If $\overline{AO}$ and $\overline{OC}$ don't make a straight line, the area of these triangles stays equal since they will still sharing the same base.