Symmetry Destroyed
A B C D is an isosceles trapezoid, and A E C is a right triangle.
Which area is larger, yellow or red?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Beautiful solution! Sorry to hijack your post, it seems like you are restricted to commenting unless you got the right solution. I understand the solutions posted here, but I don't have an idea what is wrong with mine. Can someone help me out?
Area of trapezoid = (AB+DC)/2*EC
Area of triangle = (AB*EC)/2
Now multiply by 2 and divide by EC for a better comparison:
Area of trapezoid * 2 / EC = AB + DC
Area of triangle * 2 / EC = AE * EC
Looking at the picture, AE * EC is obviously greater than AB + DC. So where did I go wrong?
Log in to reply
Why is there still an EC left from the area of the triangle after you divided it out?
Why are you comparing the area of the whole trapezoid to a triangle ABC composed of the orange area and one of the yellow triangles?
After clearing common factors EC and 2 what should be left is a comparison between EB + DC from two yellow triangle areas and AE from the orange triangle area. Dropping a perpendicular from D to AE to a new point X will reveal that AX = EB, XE = DC and AE = AX + XE = EB + DC so that the areas are equal.
Very funny that my solution goes against the title about that symmetry stuff! XD
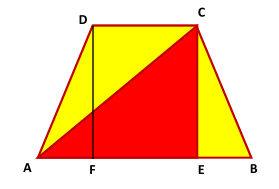 All three triangles, two yellow and one red, have the same vertical height.
All three triangles, two yellow and one red, have the same vertical height.
So if the bases can be shown to be the same, the areas will be the same as well.
The combined length of the horizontal bases of the two yellow triangles is D C + E B = F E + E B
The length of the base of the red triangle is A E = A F + F E
But because the trapezoid A B C D is symmetrical A F = E B
So the bases, and therefore the areas as well, are the same.
There's a much easier way using logic instead of pure maths: AD & CB are given as equal. If we increase the length of CB it moves to the right. In order to keep AD the same length, it has to move to the right until point D touches the line AC - at which stage the yellow area is eliminated. CB has similarly enlarged the yellow area by moving to the right until the yellow area matches perfectly the red area. AD now = AC = CB, & ACB is an equilateral triangle, divided centrally so that yellow = red.
Pandect (91 years).
Ok but if you use the math formula and substitute some appropriate numbers would this hold true?
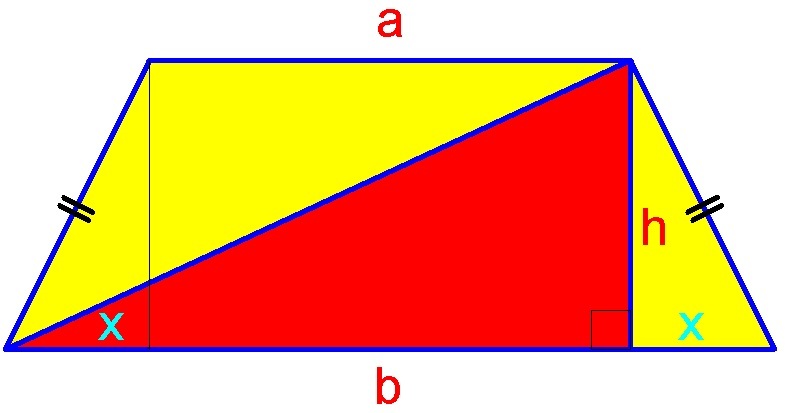 One way of solving this is to assume values, let
a
=
5
;
b
=
8
a
n
d
h
=
3
.
One way of solving this is to assume values, let
a
=
5
;
b
=
8
a
n
d
h
=
3
.
from the figure,
a + 2 x = b ⟹ 5 + 2 x = 8 ⟹ 2 x = 8 − 5 = 3 ⟹ x = 1 . 5
A t r a p e z o i d = 2 1 ( a + b ) ( h ) = 2 1 ( 5 + 8 ) ( 3 ) = 1 9 . 5
A r e d = 2 1 ( b − x ) ( h ) = 2 1 ( 8 − 1 . 5 ) ( 3 ) = 9 . 7 5
A y e l l o w = A t r a p e z o i d − A r e d = 1 9 . 5 − 9 . 7 5 = 9 . 7 5
C o n c l u s i o n : T h e a r e a o f t h e r e d r e g i o n i s e q u a l t o t h e a r e a o f t h e y e l l o w r e g i o n .
Assuming values to prove equality is not a path I would want to take. Are you taking care to show that the equality doesn't rely on the particular values you've chosen? If no, then you haven't excluded possibility that solution relies on shape of trapezoid. If yes, then you don't need the assumption.
Transform the figure into a rectangle and show that the red and yellow areas are each half of it.
1) Construct a new point F above point A and on the extension of line CD, making a right triangle ADF.
2) Triangle ADF is congruent with EBC. Color ADF yellow; remove EBC. The total area is unchanged since ADF and EBC have the same area; we have simply moved EBC to ADF.
3) The resulting rectangle AECF is divided by its diagonal, AC, into half red and half yellow.
The red and yellow areas are the same.
(Sorry, I found no instructions on how to draw diagrams)
Draw the diagram in your graphics app of choice, and use the third icon along to upload it.
Log in to reply
Adding to what Stewart said, you can use Geogebra or Desmos to post the illustration or diagram.
Transfer the yellow region on the right over to the one on the left and you get a rectangle with the top half yellow and the bottom half red. Therefore, the yellow and red regions are equal .
Thank you for saving my energy. I was going to post the same solution, (which is actually the simplest and quickest way, and easiest to visualize).
 We can use variables and properties of isosceles trapezoids to find the areas of the triangles.
We can use variables and properties of isosceles trapezoids to find the areas of the triangles.
I like your solution. It is mathematically rigourous. But could you explain how AE=x+y follows from the fact that ABCD is an isoceles trapezoid. It would add to the rigour and clarity of logic in your solution.
Log in to reply
DC || AB because if they weren't, then AD and CB could not be equal... right? Then AE = x+y.
This is the best explanation I've seen here and the only one I will uptick.
Elegant, and no semantics used as a cruch.
If we cut ∆BEC and paste it next to ∆ADC in such a way that line BC and AD overlap, then we can see that it will become a square with diagonal AC.
Hence, areas of both color will be same.
Note: This is only possible for this case (the square thing) because it is isosceles trapezoid.
Sides AD and CB are equal length so the shape is symmetrical. Triangle CEB can be "removed" and rotated to fit along AD forming a rectangle which is bisected along AC. Areas are therefore equal.
Triangle BCE can be transposed and rotated around its horizontal axis to share side BC with side AD of triangle ADC because the two sides are equal in length. Because angle BEC is 90 degrees, a rectangle is formed with (4) - 90-degree corners, which is bisected by line AC into two equal areas.
Good attempt. For clarity, can you explain why b+c=a is true?
Log in to reply
The trapezoid is isosceles; just consider the height from point D, it marks the same b on the trapezoid's major base.
improve your handwriting, please.
Note that the areas of triangles AEC and AED are equal since they have the same height and same base. Now let F be the image of point B when reflected over the perpendicular bisector of EC. Since trapezoid ABC is isosceles it can be shown that the opposite sides of quadrilateral ABFD are congruent, so it is a parallelogram with the same area as trapezoid ABCD. Also, the area of triangle AEB is equal to the area of triangle ACF, so area ACD + area CEB = area ACD + area ACF = area ADF. But EF and AD are parallel, so area AED = area AEF since they have the same base and height. Therefore, area AEC = area ACD + area CEB.
It is obviously true when DC=AB (a rectangle). And also obviously true when DC=0 (a triangle). So if it was not true in general then there would have to be a turning point in between those two extremes. But each of the three regions changes area linearly as you move from one to the other, and you cannot make a turning point from linear functions. Hence there isn't a turning point and the areas are always the same.
Here is the alternate geometric approach:
One can observe the symmetry of points B about segment C E . Including segment C F , we see that these two different-colored triangles have the same areas. We also formed parallelogram A F C D (because m ∠ C F E = m ∠ C B E ), where there are another pair of different-colored triangles also with same areas.
So because of symmetries, the red and yellow areas are the same.