Symmetry does not clear everything
As shown in the diagram below, inside a symmetrical quadrilateral, both its diagonals are drawn and two altitudes are dropped from the top vertices to the base. These segments divide the quadrilateral into eight parts, the areas of three of which are known to us: 555, 2017, 1345.
Find the area of the symmetrical quadrilateral.
The answer is 7834.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Very elegant and simple!
7834 is not the right answer. (If we don't require symmetry, then the answer is 7536.25...)
The bottom side of the trapezium is divided into 3 sections. The left one and the right one are equal. But are the side sections (marked AE and FD on Seyed's picture) bigger or smaller than the middle one (EF)?
Comparing the blue are the green areas, if the side sections were the same as the middle, the green "house" shape's bottom part, a rectangle, would be twice as big as the blue. So the blue would be smaller than half the green. That's also the case if the side sections are smaller that the middle one. But the blue triamgle is bigger that half of the green pentagon
Therefore the side sections must be (sufficiently) larger than the middle section.
That means the vertical lines (BE and CF) are cut (by diagonals) above the midpoint, making the yellow area less than 1/5 of the green area. As stated, that is not the case.
The conditions are therefore contradictory, and so the right answer is: Such trapezium does not exist.
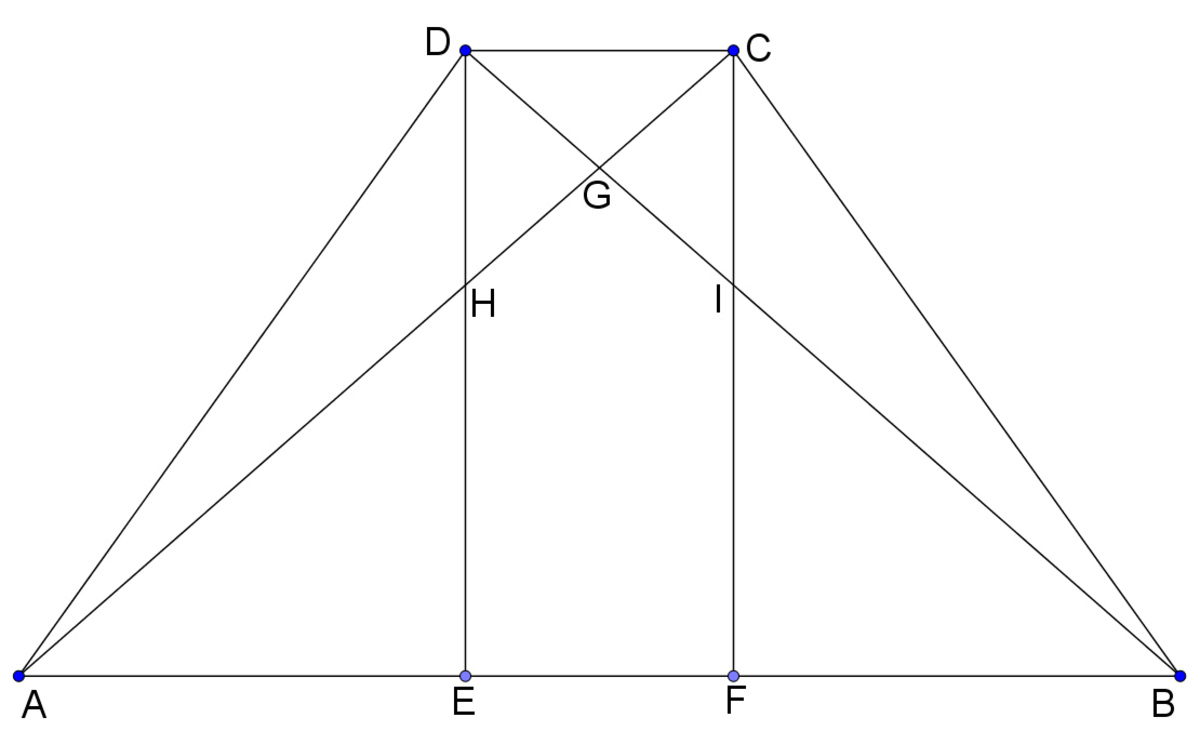
First, note that by symmetry we can say that: [ A E H ] = [ F B I ] , [ H G D ] = [ C I G ] . Using the known formulas of area, we get:
[ D C F E ] = D E ∗ C D
[ A C D ] = 2 C D ∗ E D
[ B C D ] = 2 C D ∗ E D
So
[ D C F E ] = [ A C D ] + [ B C D ]
That can be written as:
[ D C F E ] = [ H G D ] + [ C G D ] + [ I G C ] + [ E F I G H ] = [ A C D ] + [ B C D ] = [ A H D ] + [ H G D ] + [ G C D ] + [ B I C ] + [ I G C ] + [ C G D ]
By a little calculating we get: [ E F I G H ] = [ A H D ] + [ C G D ] + [ B I C ]
So the area of the symmetrical quadrilateral:
[ A B C D ] = 2 ∗ ( [ A E H ] + [ E F I G H ] + [ I G C ] ) = 2 ∗ 3 9 1 7 = 7 8 3 4
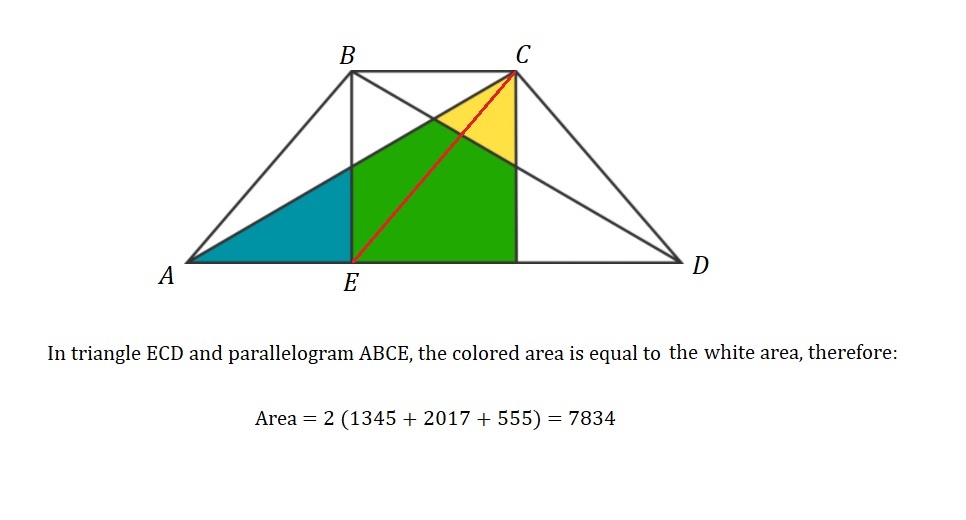
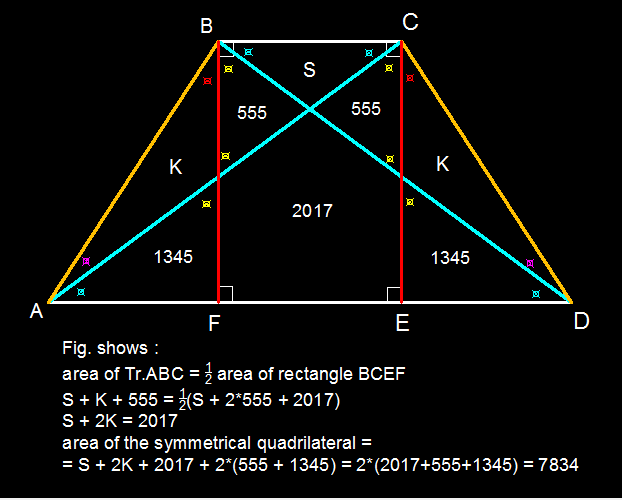

Area [ D B F ] = 2 1 ( a + b ) h = 1 3 4 5 + 2 0 1 7 + 5 5 5 = 3 9 1 7
Area [ A B C D ] = 2 1 ( A B + D C ) h = 2 1 ( a + a + 2 b ) h = ( a + b ) h = 2 [ D B F ] = 2 × 3 9 1 7 = 7 8 3 4