Symmetric Circuit

Electricity and Magnetism Level 5

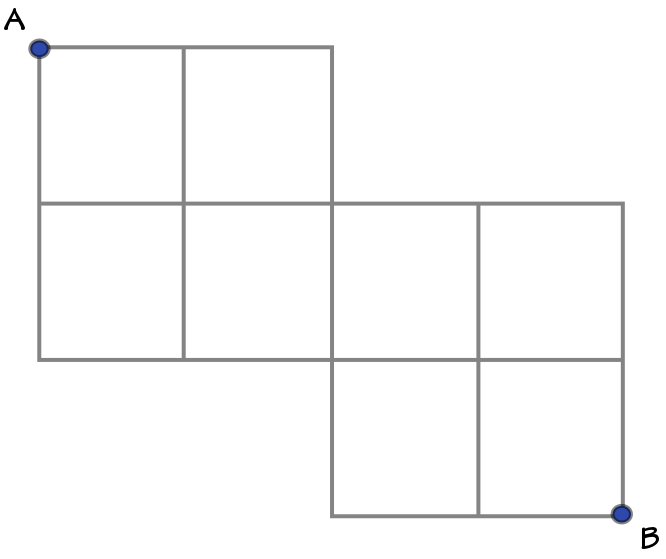
Suppose each section of wire between nodes in the circuit above has a resistance of $\SI{1}{\ohm}.$

If the equivalent resistance between points $A$ and $B$ can be represented as $\frac ab,$ where $a$ and $b$ are coprime positive integers, find $a+b.$

The answer is 105.

1 solution

Kushal Patankar
Jan 8, 2017

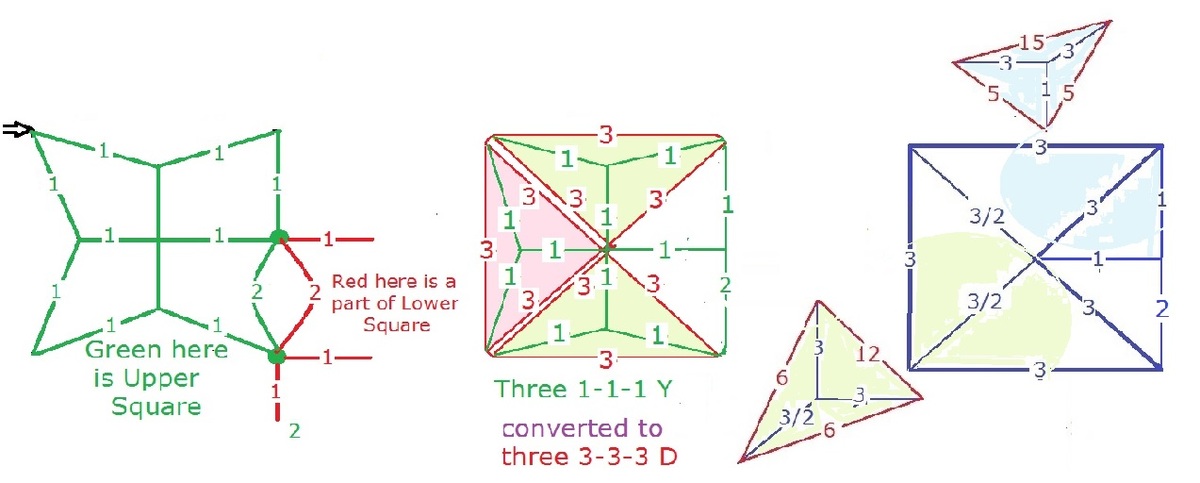
Three resistors can be joined together to form the following two circuits as shown below.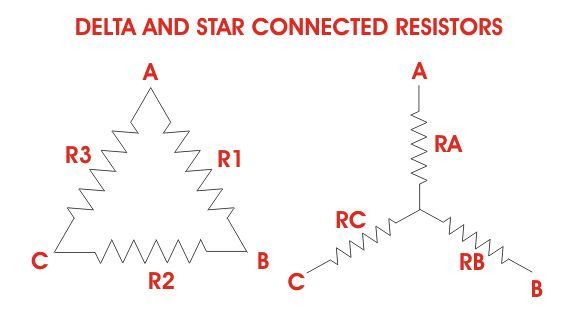

The circuit on the left is called the delta and the one on right is called star or Y form. Interestingly, these two forms are interconvertible by using the following formulas.
To convert star form into delta form
$\begin{gathered} {R_1} = \frac{{{R_A}{R_B} + {R_B}{R_C} + {R_C}{R_A}}}{{{R_C}}} \\ {R_2} = \frac{{{R_A}{R_B} + {R_B}{R_C} + {R_C}{R_A}}}{{{R_A}}} \\ {R_3} = \frac{{{R_A}{R_B} + {R_B}{R_C} + {R_C}{R_A}}}{{{R_B}}} \\ \end{gathered}$ To convert delta into star form
$\begin{gathered} {R_A} = \frac{{{R_1}{R_3}}}{{{R_1} + {R_2} + {R_3}}} \\ {R_B} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2} + {R_3}}} \\ {R_C} = \frac{{{R_2}{R_3}}}{{{R_1} + {R_2} + {R_3}}} \\ \end{gathered}$

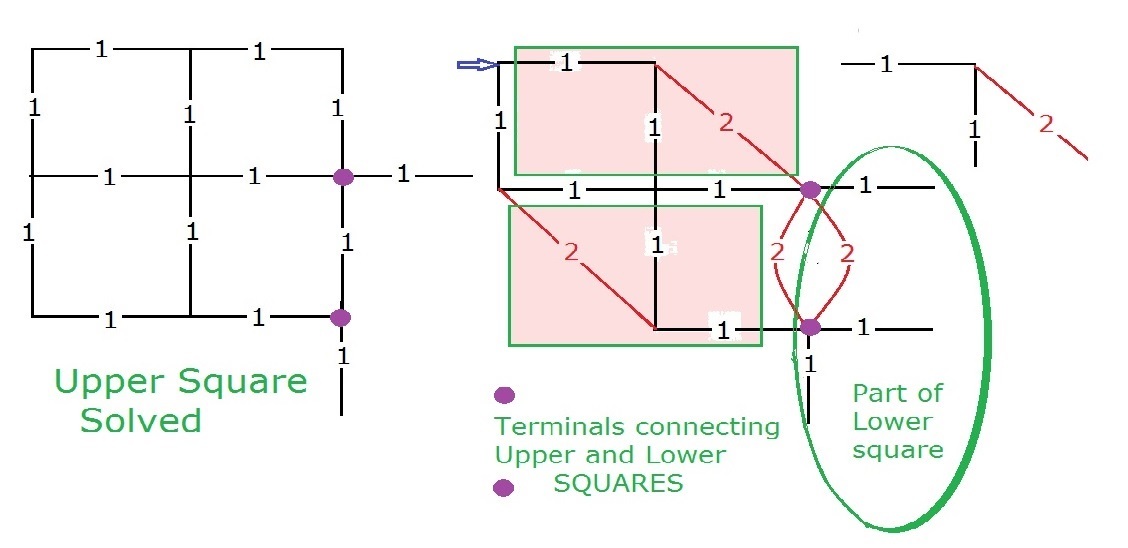
The circuit given in the problem can be solved by converting these two forms into each other.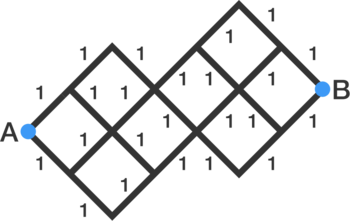
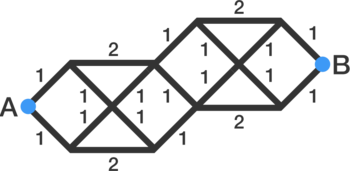
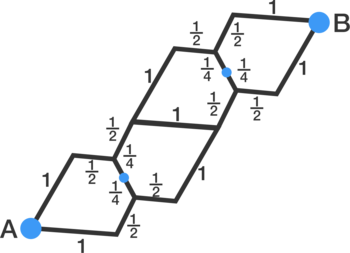
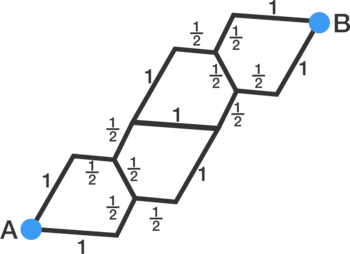
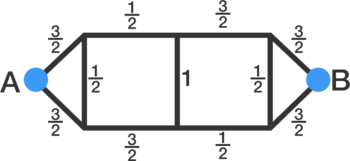
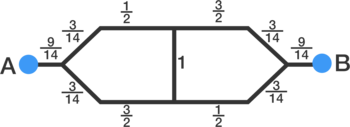
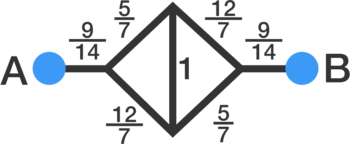
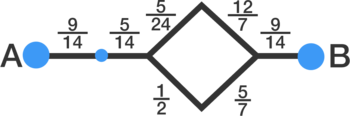
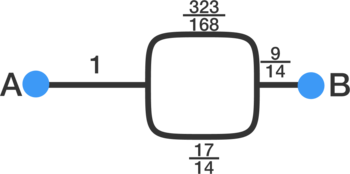
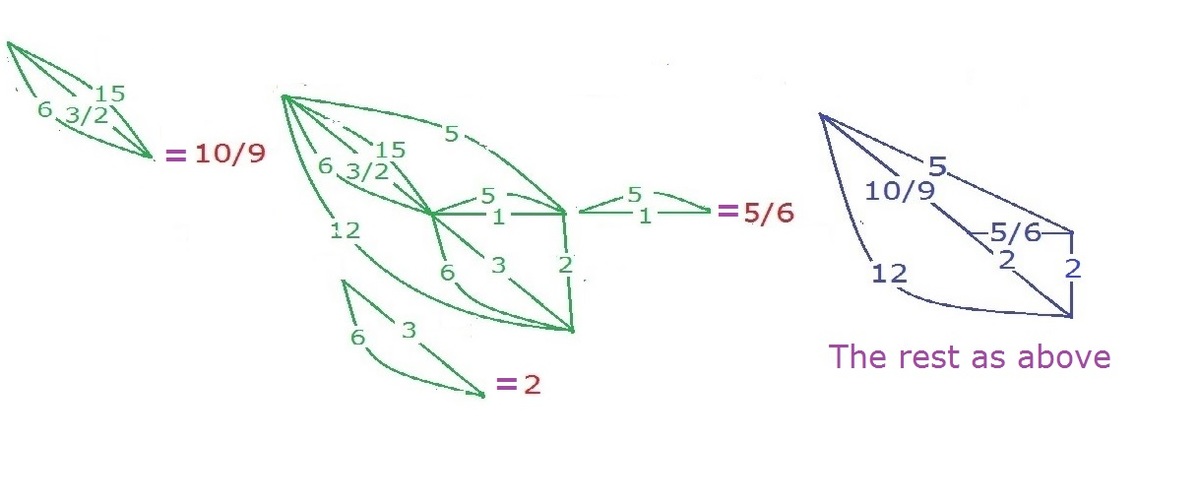
Combining the resistors in series.

Converting the delta forms (the triangles) into the star forms.

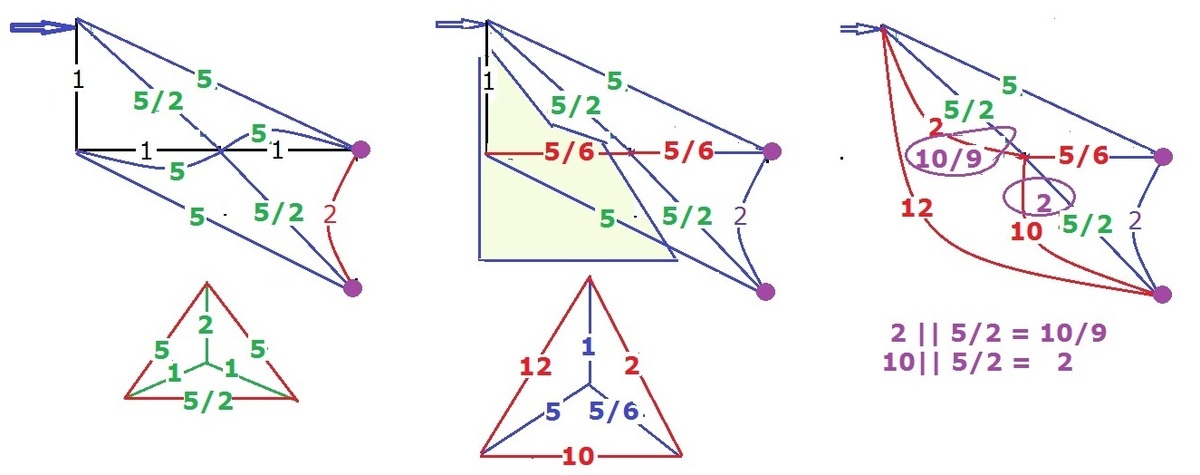
Combining the resistors in series.

Converting the delta forms (the triangles) into the star forms.

Combining the resistors in series.

Converting the delta forms (the triangles) into the star forms.

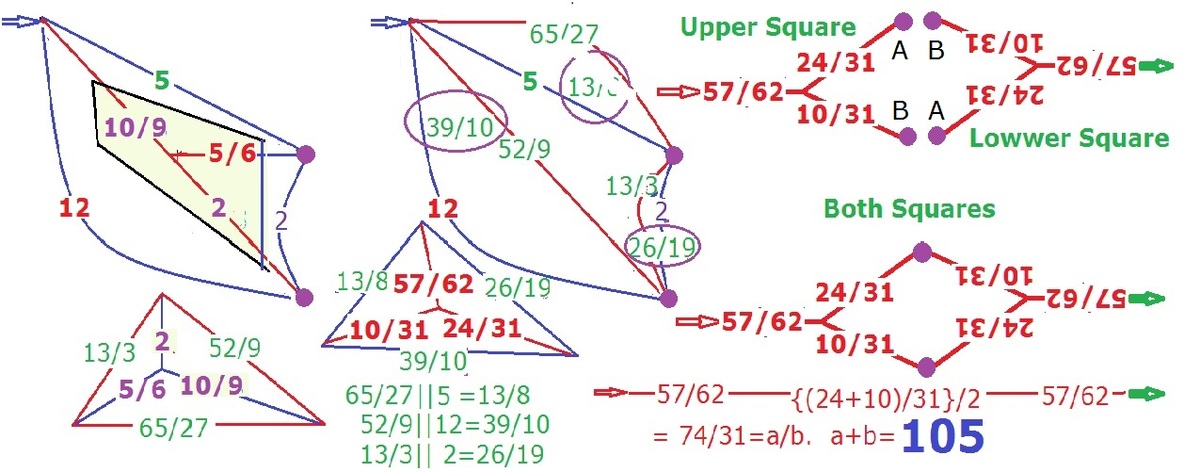
Combining the resistors in series.
Combining the resistors in parallel.
Combining the resistors in series.

Comparing the equivalent resistance, $\dfrac{a}{b}=\dfrac{74}{31}$ .
Therefore, $a=74$ and $b=31$ .
$a+b = 74+31 = \boxed{105}$ .

That's how I did it. Very well illustrated indeed. Though I wonder, can the circuit be analysed by shorting equipotential points?

Pratyush Pandey - 4 years, 4 months ago

I gave that a thought while solving the problem, didn't made much sense to me, it rather got complicated.. Pray tell if you found something...

Kushal Patankar - 4 years, 4 months ago

@Kushal Patankar there was definitely no visible symmetry in this problem that would lead to us label 2 nodes equipotential. However, there are often ways to invent symmetry when none exist (for example by breaking a resistor into two parallel ones with same terminals but double the value). I wondered if something of that sort could be done here, rather than so many star deltas.

Pratyush Pandey - 4 years, 4 months ago

My comment uses symmetry.

Niranjan Khanderia - 2 years, 11 months ago

I also did the same way..

Istiak Reza - 4 years, 4 months ago

This solution was just absolutely beautiful. I don't think anyone could have explained this better than you . Also a huge thanks for teaching me this star-delta conversion. :)

saharsh rathi - 4 years, 4 months ago

It wasn't me actually I posted handwritten version of the same solution, somebody from brilliant fancied it up. All appreciation to Brilliant.org.

Kushal Patankar - 4 years, 4 months ago

You cant use star delta conversion when a and c are joined by other resistors in delta form if we see through symmetry current should not pass through 1 ohm resistor that is in middle joining the two squares

aditya ranjan - 4 years ago

@Kushal Patankar ,

Can't i do this with symmetry considerations only?

Priyanshu Mishra - 3 years, 5 months ago

Here is symmetry like considerations. Only that lower square is upside down with respect to upper and the connecting resistance is split to make the system symmetry like. I have used Star-Delta transformations, and last Delta-Star.
Star-Delta transformations reduces number of nodes.
While Delta-Star is used to transform into series-parallel.
I missed this problem mainly since I did not at first split the 1 ohm connector in to 2 | | 2. The structure of Upper and Lower squares are the same. There is a 1 ohm resistor between the two connector nodes, say A and B, connecting the two squares.
After splitting the 1 ohm into two 2 || 2, we separate the two squares. Solve the Upper square net.
Lower square too will have the same solution.
Since with respect to Upper, Lower one is up side down, we connect Upper A with Lower B, and Upper B with lower A to get a net equivalent to the original net.
The transformation formula are so common and can be easily found in web, so I have not given them here.

Alternate solution of the Y-D transformations. Rest as above.

Niranjan Khanderia - 2 years, 11 months ago

Symmetric Circuit

The answer is 105.

1 solution

1 pending report

Vote up reports you agree with