Symmetry in geometry
Geometry
Level
pending
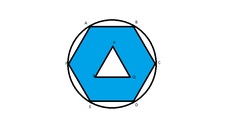ABCDEF is a regular hexagon and PQR is an equilateral triangle of side a. The area of the blue-colored portion is X and CD:PQ::2:1. Find the area of the circle circumscribing the hexagon in terms of X.
(2π/3√3)X
2√3πX
(42π/5√3)X
(16π/23√3)X
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Area of equilateral triangle = (√3/4)a² Area of regular hexagon= 6 (√3/4)(r²)= 6 (√3/4)(2a)²= 6√3a²
X= 6√3a²-(√3/4)a²=( 23√3)(a²)/4
» a²= 4X/( 23√3)
For a regular hexagon and a circumscribing circle , radius of circle=side of hexagon.
Area of circle=π(2a)²= 4πa² = 16πX/( 23√3)