Symmetry of semi circular wire

It’s not hard to see that the moment of inertia must be non-zero, regardless of the angle. There’s only one possibility that allows that to happen.

The moment of inertia is given by $\displaystyle I = \int_a^b r^2\ dm$ , where $r$ is the perpendicular distance from the axis of rotation $CD$ to the infinitesimal mass element $dm$ .

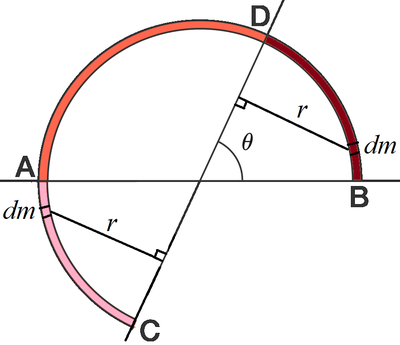
Since $r^2\ dm$ is even we can replace each infinitesimal mass element $dm$ in the arc $BD$ (brown) with an infinitesimal mass element $dm$ in the arc $AC$ (pink) with the same perpendicular distance from $CD$ . Therefore, in effect, the moment of inertia about the axix $CD$ is the same as that about $AB$ , which is equal to $\boxed I$ .

If we add another half ring below the given semi ring, by symmetry, the moment of inertia of the complete ring will be the same for both the axis AB and CD.

Also, the moment of inertia for both the halves of the rings is the same for both the axis AB and CD. Thus, if the moment of inertia of semi ring about AB is I, then for the complete ring it must be 2I. It will thus be 2I for axis CD as well and for half of the ring, it will be I only.

Moment of inertia is extensive property, i.e. can be the sum of moment of inertia of parts. The part of the semi-circular wire that is complement to \pi of the \theta part can be moved by central symmetry about the point at the intersection of AB and CD. Then you get back a semi-circular wire on "right" side of CD, similar to that "above" AB. So, inertia has not changed.

In all of the answers where the moment of inertia is multiplied by sines and cosines, the value would be zero for particular angles. This is not acceptable because no matter how the axis is rotated about its midpoint, there is always some mass at a finite distance from the axis, so the moment of inertia must not be zero. The only answer that isn’t wrong is that the moment of inertia doesn’t depend on the angle.

If you reflect the part to the left of axis $CD$ about the origin, you get the same situation as when the rotational axis is $AB$ . Since this operation does not change the distance between the parts of the ring and the axis of rotation, the moment of inertia also remains the same: $I$ .

Rigorous Calculation Below:

Assume the mass of the semicircle ring to be $M$ , the radius is $R$ , linear density is $\sigma$ , and it has been known that the moment of inertia of the semicircle ring is $I=\dfrac12 MR^2$ . Therefore, using polar coordinate $\rho,\alpha$ to represent: $M=\pi r\sigma,dm=\sigma Rd\alpha$ , then the distance from a small point to $CD$ is $R\sin(\alpha-\theta)$ .

The moment of inertia relative to the axis $CD$ is

$\begin{aligned}I_{CD}&=\int_0^\pi(R\sin(\alpha-\theta))^2 \sigma Rd\alpha=\dfrac\pi2 R^3\sigma\end{aligned}$

Since $\sigma=\dfrac{M}{\pi R}$ , the moment of inertia is $I_{CD}=\dfrac12 MR^2=I$ .