Drawing In The Argand Plane
∣ z + 1 + i ∣ ∣ z ∣ = 2 = 3 The above system of equations (where i = − 1 ) has
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Let be z = a + i b , so we have:
z + 1 + i = ( a + 1 ) + ( b + 1 ) i
∣ z ∣ = a 2 + b 2 ⇒ a 2 + b 2 = 3
∣ z + 1 + i ∣ = ( a + 1 ) 2 + ( b + 1 ) 2 ⇒ ( a + 1 ) 2 + ( b + 1 ) 2 = 2
Raising both equations to the square power we obtain:
a 2 + b 2 = 9
( a + 1 ) 2 + ( b + 1 ) 2 = 2
Let's develop the second equation:
a 2 + 2 a + 1 + b 2 + 2 b + 1 = 2 ⇒ a 2 + 2 a + b 2 + 2 b = 0
But the first equation says a 2 + b 2 = 9 , so:
a 2 + 2 a + b 2 + 2 b = 0 ⇒ 9 + 2 a + 2 b = 0 ⇒ ( a + b ) = − 2 9
being ( a + b ) 2 = a 2 + b 2 + 2 a b we obviously have that a 2 + b 2 = ( a + b ) 2 − 2 a b
so:
( − 2 9 ) 2 − 2 a b = 9 ⇒ 8 1 / 4 − 2 a b = 9 ⇒ a b = 4 5 / 8
So we can build a new equation:
x 2 + ( a + b ) x + a b = 0 ⇒ x 2 − 2 9 x + 8 4 5 = 0
that has no solutions, being Δ = 4 8 1 − [ 4 × 8 4 5 ] = 4 8 1 − 2 4 5 = − 4 9
Graphical solution is much easier!
Why does ∣ z ∣ = a 2 + b 2 ?
Log in to reply
|z| is called "modulus" of the complex number a + i b . It represents the distance between origin of the complex plan and the point which coordinates are "a" on the real axis and "b" on the complex one. It is the same thing than measuring the distance between the origin of the real plan and any point P(x, y) on it.
Using Triangular Inequality
∣ z ∣ − ∣ i + 1 ∣ ≤ ∣ z + 1 + i ∣ ≤ ∣ z ∣ + ∣ 1 + i ∣
Also ∣ z ∣ = 3
3 − 2 ≤ ∣ z + 1 + i ∣ ≤ 3 + 2
But 2 does not lie in above range .Hence no solutions
We can solve the two equations considering the complex number z as z = x + i y .
It is a known fact that ∣ z ∣ = x 2 + y 2
The given equations are:
- ∣ z ∣ = 3
- ∣ z + 1 + i ∣ = 2
So equation ( 1 ) becomes
x 2 + y 2 = 3
⇒ x 2 + y 2 = 9
which is the equation of a circle of radius 3 units centered at the origin.
And equation ( 2 ) becomes
∣ x + i y + 1 + i ∣ = 2
⇒ ∣ ( x + 1 ) + i ( y + 1 ) ∣ = 2
⇒ ( x + 1 ) 2 + ( y + 1 ) 2 = 2
⇒ ( x + 1 ) 2 + ( y + 1 ) 2 = 2
which is the equation of a circle of radius 2 units centered at ( − 1 , − 1 ) .
For understanding how we get to know the radius and center of the circle, refer Equation of a Circle
When the graphs of these two equations are plotted in the x y plane they look like this : -
The blue circle is the graph of equation ( 1 ) and the red circle is the graph of equation ( 2 )
We can clearly see that they do not intersect anywhere in their domain, which means there is no coordinate ( x , y ) that satisfies both the equations simultaneously . Hence the two equations have no common solution.
For the more rigorous algebraic solution to this answer, you can refer the answer given by Giorgio de Fornasari.
Since |z| = 3, z must be -3 or 3. From this the two equations can be simplified to be |4 + i| = (2)^(1/2) and |-2 + i| = (2)^(1/2). We know that a^2 + b^2 = |a + bi|^2, so 16 + 1 = |4 + i|^2, so (17)^(1/2) = |4+ 1|, since (17)^(1/2) does not equal (2)^(1/2), this equation is wrong. Next |-2 + i| = (-2)^2 + (1)^2 = 4 + 1 = 5, so (5)^(1/2) = |-2 + i|. Since (5)^(1/2) does not equal (2)^(1/2) this equation does not work either. Since both possible options for these equations have been exhausted there is no solution.
Moderator note:
The first line is not true. For example, ∣ 1 + 8 i ∣ = 3 .
If z has imaginary part equal to 0, then it must be -3 or 3, but if not, it can be any complex number a+bi such that (a^2+b^2)^(1/2)=3 for real numbers a and b. There is an infinite number of z's which satisfy this, all of which lie in the complex plane on a circle centered at the origin with radius equal to 3. Think about |z| as the distance of z from the point (0,0) in the complex plane.
The first line is not true. For example, ∣ 1 + 8 i ∣ = 3 .
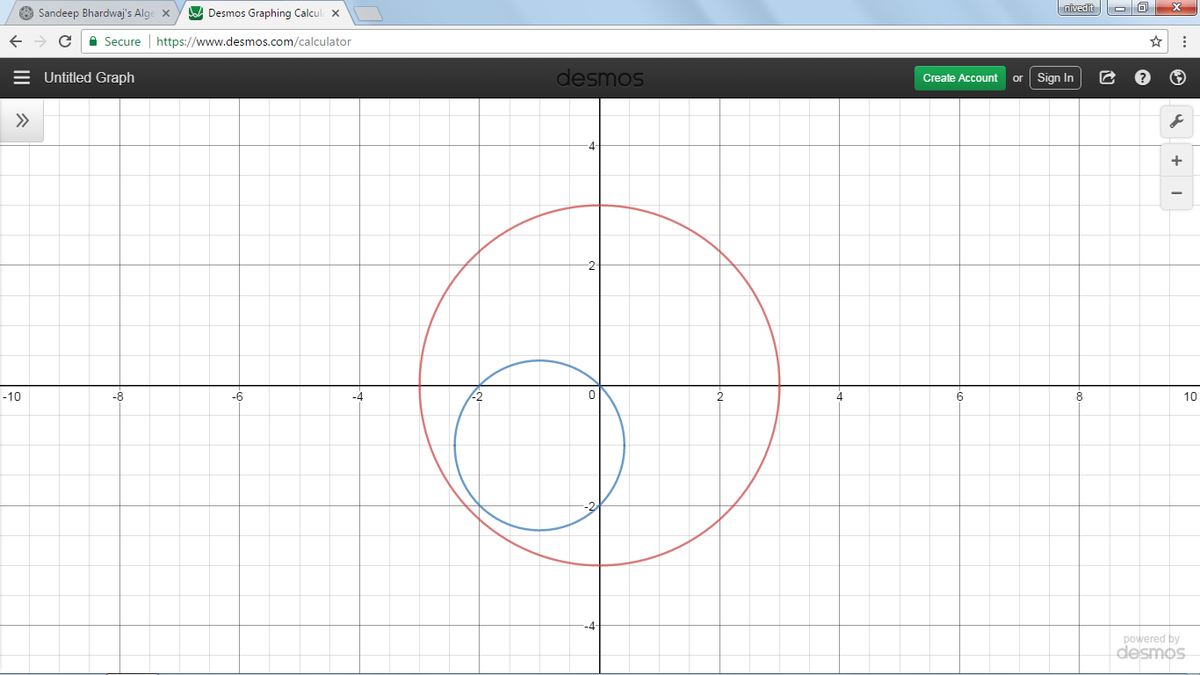
Partial Solution:
The first equation represents a circle with radius Sqrt(2) centered at (-1,-1)
The second equation is a circle of radius 3 centered at the origin.
Clearly, they do not touch each other, which is why there are no solutions