System of Non-collinear Points in a Plane!

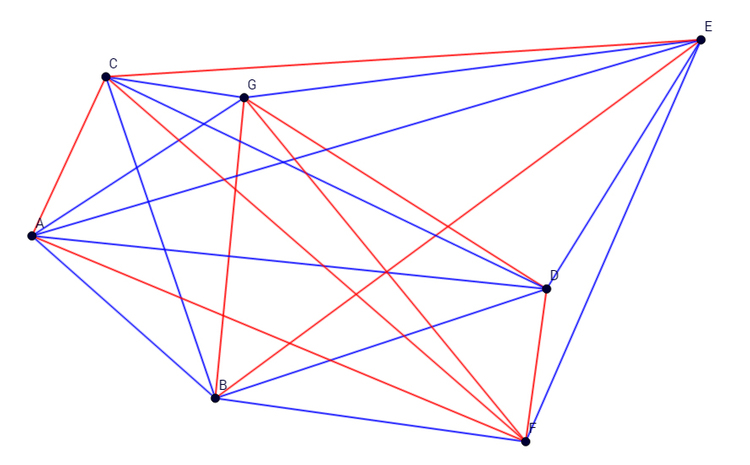There are seven points in a plane, no three of which are collinear. Every point is connected to every other point by either a red or a blue line segment. What is the minimum number of monochromatic triangles that can be present in such a figure? Select the correct option.

Bonus: Generalize, if possible, the minumum number of monochromatic triangles for such a problem scenario as of above, given that there are $n \geq 3$ points in the plane.

Note: The above figure is just a possible case for $n=7$ and is mentioned for reference.