System of Particles on a wedge!
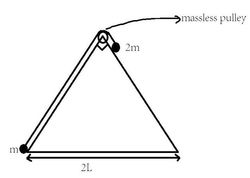 A right angled isosceles triangular wedge of mass
m
is placed on a smooth horizontal surface. Two point like masses
m
&
2
m
, tied to each other by a thread, are placed on the wedge. Friction & masses of the thread & pulley are negligible. The bodies are released at
t
=
0
. The distance moved by the wedge until the "instant
2
m
reaches the bottom of wedge" is
A right angled isosceles triangular wedge of mass
m
is placed on a smooth horizontal surface. Two point like masses
m
&
2
m
, tied to each other by a thread, are placed on the wedge. Friction & masses of the thread & pulley are negligible. The bodies are released at
t
=
0
. The distance moved by the wedge until the "instant
2
m
reaches the bottom of wedge" is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
nicely done! upvoted ⌣ ¨
@Tanishq Varshney Just add a point in your solution to make it more clear for others. Since there are no net external forces horizontally acting on the system, center of mass will remain at rest in the horizontal direction.
Log in to reply
Nishant sir can you give detail solution if there acts no force . Why cm initial =com final. Some mathematical arguments.
We can solve it in one more way although with a similar concept as used by Tanishq Varshney .
If the Wedge moves backward by a distance of x then both the point masses will move by (L-x) in forward direction.
As the center of mass doesnot move in the horizontal direction, Therefore it can be written that
Δ
x
c
m
=
(
m
1
Δ
x
1
+
m
2
Δ
x
2
+
m
3
Δ
x
3
)
/
m
t
o
t
a
l
=
0
=> 2m(L-x)+m(L-x)-mx=0
=>x=3L/4
I did the same but made a silly mistake in my calculations. Uhrrr!
Let centre of mass of the system be denoted as r c m
Initially
( r c m ) i = 4 m m × 0 + 2 m L + m L
when the 2 m reaches bottom of wedge , let the distance moved by centre of mass be x and this new position be denoted as ( r c m ) f . we have to basically find x
( r c m ) f = 4 m m ( L − x ) + 2 m ( 2 L − x ) + m ( L − x )
Since no external force acts on the system horizontally so centre of mass remains at rest so
( r c m ) i = ( r c m ) f
solve for x , we get
x = 4 3 L