System Voltage Profile
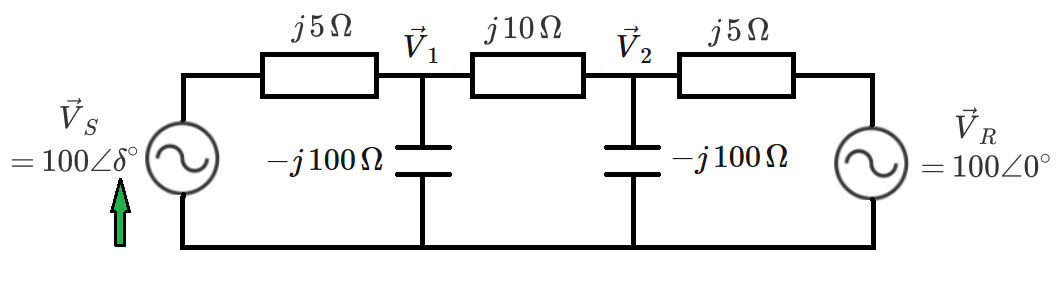
Two AC voltage sources feed the two ends of a transmission line, which is modeled as a pi circuit as shown. The source on the left has a phase angle of , in degrees, and the source on the right has a phase angle of zero.
It is known that lightly-loaded transmission lines tend to experience over-voltage conditions due to the shunt parasitic capacitance. Consequently, power utilities often switch in shunt inductances to offset this effect during periods of light load (such as at night). Such inductors are not present in this particular system. The loading (amount of active power flowing across the line) increases with the load angle .
What is the smallest positive integer value of (in degrees) for which the magnitude of is less than volts?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Considering the following polarities and current orientations:
One gets from applying Kirchhoff's circuit laws :
j ⋅ ⎣ ⎢ ⎡ − 9 5 1 0 0 0 1 0 0 − 1 9 0 1 0 0 0 1 0 0 − 9 5 ⎦ ⎥ ⎤ ⋅ ⎣ ⎢ ⎡ i 1 i 2 i 3 ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ 1 0 0 ∠ δ 0 − 1 0 0 ⎦ ⎥ ⎤
⎣ ⎢ ⎡ i 1 i 2 i 3 ⎦ ⎥ ⎤ = − 7 4 1 j 1 0 ⋅ ⎣ ⎢ ⎡ 3 2 2 ∠ δ − 4 0 0 3 8 0 ∠ δ − 3 8 0 4 0 0 ∠ δ − 3 2 2 ⎦ ⎥ ⎤
Since:
V 1 = − j 1 0 0 ( i 1 − i 2 )
Then:
V 1 = 7 4 1 1 0 0 0 ⋅ ( 5 8 ∠ δ + 2 0 )
So:
∣ V 1 ∣ = 7 4 1 1 0 0 0 ⋅ ( 5 8 cos ( δ ) + 2 0 ) 2 + ( 5 8 sin ( δ ) ) 2 < 1 0 0
1 0 0 ⋅ ( 3 7 6 4 + 2 3 2 0 cos ( δ ) ) < 5 4 9 0 8 1
cos ( δ ) < 0 . 7 4 4 3 1 4 6 5 5
So :
δ > 4 1 . 8 9 ∘
Or:
δ m i n = 4 2 ∘