Systems of equations

Adding the $5$ equations, we obtain

$(4x^2-4x+1)+(4y^2-4y+1)+(4u^2-4u+1)+(4v^2-4v+1)+(4w^2-4w+1)=0$

Then,

$(2x-1)^2+(2y-1)^2+(2u-1)^2+(2v-1)^2+(2w-1)^2=0$

Due to the fact that $x,y,u,v$ and $w$ are all real numbers, we obtain

$x=y=u=v=w=\dfrac{1}{2}$

Finally,

$x+y+u+v+w=5(\dfrac{1}{2})=2.5$

First... it is simply to know that $u,v,w,x,y>0$ .

Now, WLOG, We assume $u \geq v \geq w \geq x \geq y$ .

Then $x^2+u^2+v^2+w^2 \geq 4y^2$ $4y-1 \geq 4y^2$ $0 \geq (2y-1)^2$ The innequality above has solution if $0 = (2y-1)^2$ $\frac{1}{2} = y$ Then $x^2+u^2+v^2+w^2 \geq 4x^2$ $4y-1 \geq 4x^2$ $4.\frac{1}{2}-1 \geq 4x^2$ $1 \geq 4x^2$ $1 \geq 2x$ $\frac{1}{2} \geq x$ Because $x \geq y$ , we can conclude that $x = \frac{1}{2}$

Then $x^2+u^2+v^2+w^2 \geq x^2+3w^2$ $4y-1 \geq \frac{1}{4}+3w^2$ $1 \geq \frac{1}{4}+3w^2$ $\frac{3}{4} \geq 3w^2$ $1 \geq 4w^2$ $1 \geq 2w$ $\frac{1}{2} \geq w$ Because $w \geq x$ , we can conclude that $w = \frac{1}{2}$

Then $x^2+u^2+v^2+w^2 \geq x^2+w^2+2v^2$ $4y-1 \geq \frac{1}{4}+\frac{1}{4}+2v^2$ $1 \geq \frac{1}{2}+2v^2$ $\frac{1}{2} \geq 2v^2$ $1 \geq 4v^2$ $1 \geq 2v$ $\frac{1}{2} \geq v$ Because $v \geq w$ , we can conclude that $v = \frac{1}{2}$

And finally $x^2+u^2+v^2+w^2 = 4y-1$ $3.\frac{1}{4}+u^2 = 1$ $u^2 = \frac{1}{4}$ $u = \frac{1}{2}$ So the solution is $(u,v,w,x,y)=(\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2},\frac{1}{2})$ . The solution satisfies our assumption and the equations above. So $u+v+w+x+y=5.\frac{1}{2}=\frac{5}{2}=\boxed{2.5}$

It is easy to see that each of $x,y,u,v,w$ must be positive.

Imagine now the points $x,y,u,v,w$ on a hypercube that has one corner in origo 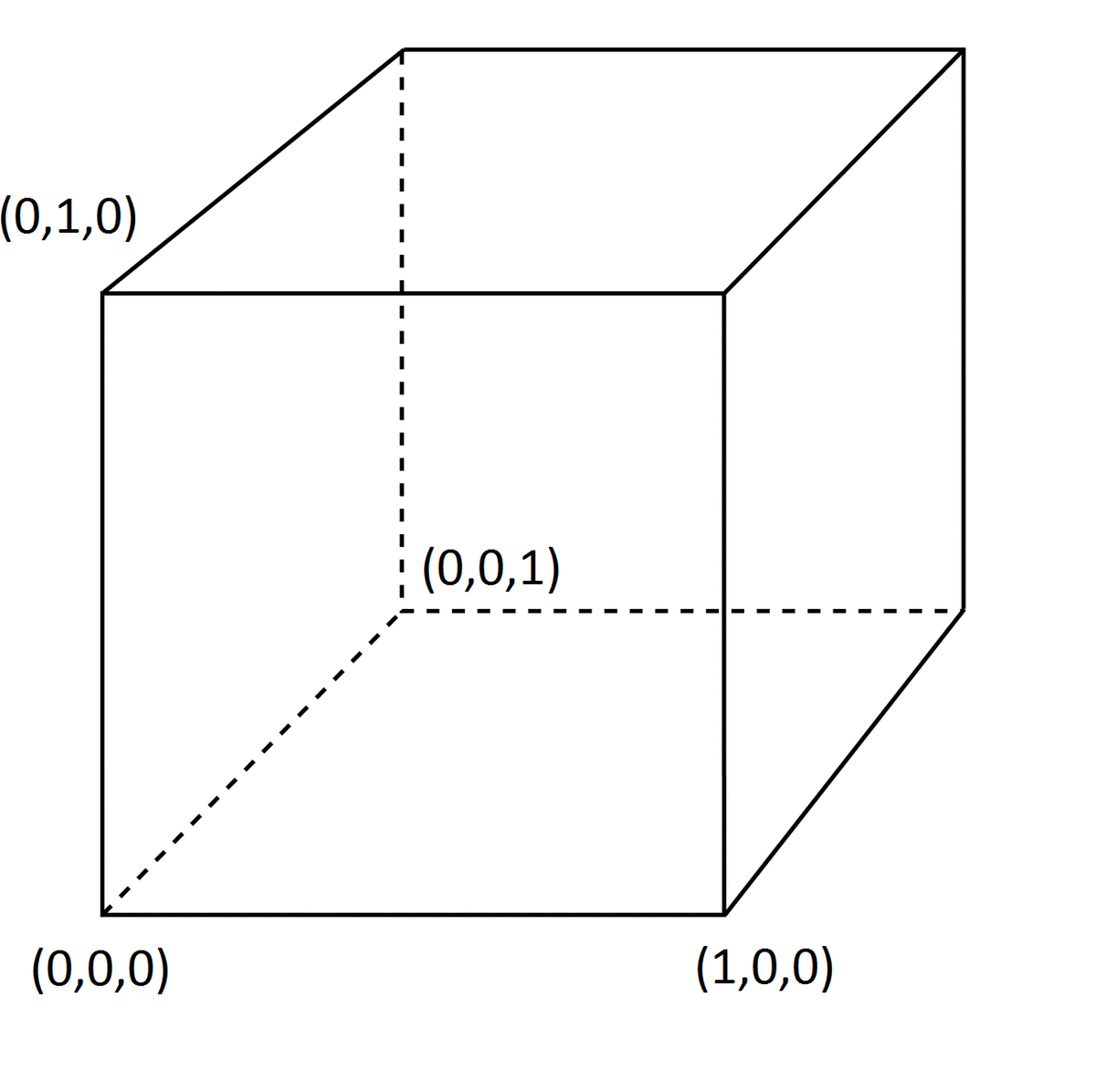(My family is very poor and we could not afford the two extra dimensions missing in this image)

Consider then for example the equation

$y^2+u^2+v^2+w^2=4x-1$ What this means geometrically is that we can permutate the axises $y,u,v,w$ of our hypercube freely and we still have a solution (for example if $(a,b,c,d,e)$ is a solution then $(a,b,c,e,d)$ is also a solution.). These correspond to reflections w.r.t a plane of hypercube (imagine this with the help of the following image). We are then interested in the set of points that are symmetric w.r.t all such planes. These correspond to the intersections of the planes. 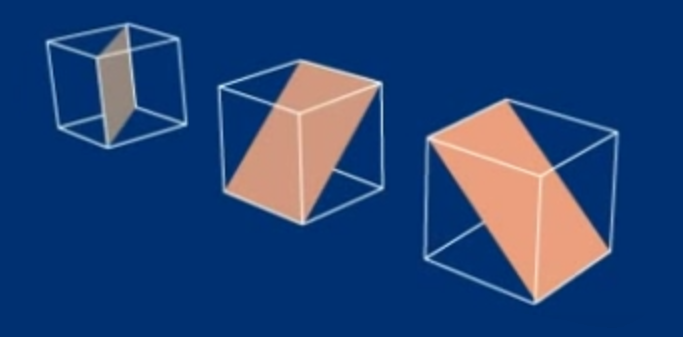In 3d (and indeed generally) this intersection is the line from origo to the opposite corner, in our case this is $(0,0,0,0,0) \to (1,1,1,1,1)$ . Hence all of the solutions lie on the diagonal.

So the solutions are of the form $(c,c,c,c,c)$ , then we have simply from any equation

$4c^2-4c+1=0$ so $c=1/2$ . Due symmetry this automatically fulfills all equations. So the answer is $5c=2.5$