Table seating reviewed

Computer Science Level 3

You may have encountered a problem on Brilliant about seating people around a long table made out of n-sided tables of equal side lengths. This one goes a little bit further.

You are preparing a big feast. You need to create one long table from small regular shaped n-lateral tables. We illustrate this in the picture bellow. You may seat one and only one person at each side of the small table.

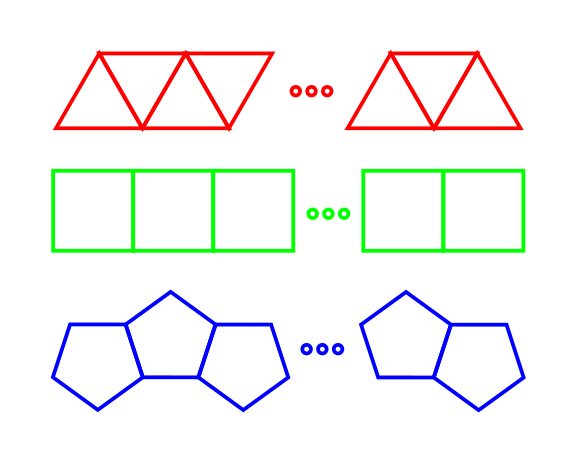
What is the sum of all posible side numbers (triangle = 3, square = 4 etc.) you can use to seat 112 people?

Although this can be done on paper, try to use some code and let the computer do the job!

The answer is 232.

7 solutions

Chris Lewis
Jun 5, 2019

One obvious solution is a single, $112$ -sided table.

For the other cases, we have more than one table.

Say we put $n$ small, $s$ -sided tables together to form the large table.

The two end tables have $s-1$ seats available. The other $n-2$ tables have $s-2$ seats available. So we need

$2(s-1)+(n-2)(s-2)=2+n(s-2)=112$ , with $n>1$ .

This means we're looking at proper divisors of $110$ :

$s-2 \in \{1,2,5,10,11,22,55\}$

Summing all possible $s$ (including the single table solution) gives the answer $\boxed {232}$ .

To find a pattern we will look into the example of, number of sides = 5

For one table, $Sides Available = 5$

For two tables, one side of each table is joined, thus unusable, so the result would be, $SidesAvailable = (5 - 1) \times 2 = 8$

For three tables,

One side of each end table is joined with an adjacent table, so only 4 sides are usable. $SidesAvailable = 2 \times ( 5 - 1 )$
And for each table with two adjacent tables, will have two adjoined sides thus only 3 sides are usable, $SidesAvailable= 1 \times ( 5 - 2 )$
$Total Sides Available = 2 \times (5 - 1) + 1 \times ( 5 - 2 ) = 11$

For n - tables,

Each end table will contribute $2 \times ( 5 - 1 )$ , and middle tables will contribute $(5 - 2)$ for each table, thus $(n - 2) \times ( 5 - 2 )$ .
Finally, $Total SidesAvailable = 2 \times (5 - 1) + (n - 2) \times (5 - 2)$
Sides Required = 112.
So, $112 = 2 \times ( 5 - 1 ) + ( n - 2 ) \times ( 5 - 2 )$ .
On solving, we get $n = 36.66...$
Since it is not a whole number, it will not contribute to the result.

So the final problem would be,

$n$ = number of shapes,

$m$ = number of sides of the shapes

$112 = 2 \times ( m - 1 ) + ( n - 2 ) \times ( m - 2 )$

On rearranging, we get, $m = \frac{ 112 - 2 \times ( n - 1 )}{ n - 2 }$

Thus the Python Code will be

# Final Result
result = 0
for number_of_sides in range(3, 113):
    number_of_shapes = 112 - 2 * ( number_of_sides - 1 )
    number_of_shapes /= ( number_of_sides - 2 )
    # Since the end shapes are not taken into account
    number_of_shapes += 2
    # Only add result, if number of shapes is a whole number
    if number_of_shapes == number_of_shapes // 1 :
        result += number_of_sides
print('Result = ', result)

Output :

Result = 232

Arvind Singh Rawat - 1 year, 6 months ago

Did you want to post this as a separate solution or a comment to Chris Lewis' solution?

Amogha Pokkulandra - 1 year ago

Martin Ošmera
Jun 5, 2019

First, we need to find the pattern. Except for the first and last table, you can seat $n-2$ people around each small table. This means, that for n-sided table, number of available seats $S = T(n-2) + 2$ , where $T$ is the number of used tables. Thus the folowing must apply: $(n-2) | (S-2)$ . Now, we can write a function in python:

    def guesttables(guests): #This function will print yes or no for every number of sides smaller or equal to number of guests.
        number = 0 #holds the number of possible numbers
        sumi = 0 #holds the total sum of possible numbers
        for i in range(3,guests + 1):
            print(i,end=": ")
            if (guests-2)%(i-2)==0: #tests for every i
                print("yes")
                number += 1
                sumi += i
            else:
                print("No")

        print("There are " + str(number) + " different equaly-sided tables you can use in a row o seat " + str(guests) + " people and all the numbers of different possible side numbers add up to " + str(sumi) + ".")

The output after calling

1	`guesttables(112)`

looks like this:

1	`There are 8 different equaly-sided tables you can use in a row o sit 112 people and all the numbers of different possible side numbers add up to 232.`

I have a different answer. 225. The different n-laterals are following:
112 (one 112-gon, 0 places lost)
57 (two 57-gons, 2 places lost),
24 (five 24-gons, 8 places lost),
13 (ten 13-gons, 18 places lost),
12 (eleven 12-gons, 20 places lost)
4 (55x 4-gons, 108 places lost)
3 (110x 3-gons, 218 places lost)

112+57+24+13+12+4+3=225 mistake?

Edit: 22x 7-gons added to the list (42 places lost) 225+7=232

Eric Scholz - 2 years ago

Alex Burgess
Jun 7, 2019

Lets have $m$ $n$ -sided tables.

There are $mn$ total sides, of which $2(m-1)$ are paired together. Thus leaving $(n-2)m+2$ spaces.

Hence, $(n-2)m = 110$ .

$m,(n-2) \in {1,2,5,10,11,22,55,110}$ .

$n \in S = {3,4,7,12,13,24,57,112}$ with $sum(S) = 232$ .

Didn't use Python as at the point I split the problem down to something to program all I was doing was factorising, but with a larger amount of people, a good factoring algorithm would be good to implement.

Niraj Sawant
Sep 23, 2019

Sorry I don't know how to post python solution.Please let me know.

Here is the code -

count = 0

for n in range( 3 , 113 ):

    if 110 % (n - 2) == 0:

            count += n

print (count)

cool, could you hint me " 110%(n-2) " , what does mean ?

eric lee - 1 year, 3 months ago

Sorry for this late, '%' operator is used to calculate modulo in Python

Niraj Sawant - 9 months, 1 week ago

K T
Jun 18, 2019

k n-gons offer seat to $(n-2)k+2$ people. 110=2×5×11 has 8 divisors $1,2,5,10,11,22,55,110$ , so the sum of possible n is $8×2+ 1+2+5+10+11+22+55+110=232$ . I do not see why coding would save work.

Joël Ganesh
Jun 7, 2019

Another possible solution (made in C#), however not as efficient as the solution from the original poster.

using System;

namespace Brilliant
{
    class TableSeatingInPython
    {
        static void Main()
        {
            int n = 0; // This will be the resulting sum.
            for (int i = 3; i < 113; i++)
            {
                int k = 0;
                // The number i + (i - 2) * k is exactly the number of seats when using a table with i sides, 
                // with k copies attached to it. I will leave the proof of this as an easy exercise for the reader.
                while (i + (i - 2) * k < 112)
                    k++;
                if (i + (i - 2) * k == 112) // If this is true, then a table exists out of tables with i sides -> add i to n.
                    n += i;
            }
            Console.WriteLine(n.ToString());
            Console.ReadKey();
        }
    }
}

Output when it runs:

Richard Desper
Jun 5, 2019

i = 3

solutions = []

while i < 113:

diff = i - 2  #diff is the number of people added to the big table when each new i-gon is added on the end

j = i

while j < 113:  #this loop adds more i-gons to the big table

    j = j + diff

    if (j == 112):

        print(i,diff,j)  #just for my edification 

        solutions.append(i)   

i = i+1

solutions [3, 4, 7, 12, 13, 24, 57]

For answer: sum up entries in solutions list.

So...the answer is 120! Whoops, I forgot the 112-sided table! The answer is 232!

Table seating reviewed

The answer is 232.

7 solutions

0 pending reports