This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
The enunciantion doesn't let clear to us that we can drawn straight lines which don't have to starts and ends necessarily about the sides of the triangle.
Log in to reply
Actually, the failed attempts shows that it is an option.
Any other attempt ?
so this is a trial and error problem? you haven't shown us HOW you arrived at the solution.
Can we show it's impossible to do so in less than 7 moves?
is there like a formula
I saw that answer on Ted Ed.
It can be done by joing midpoints of every side and repeating with triangles being formed
Moderator note:
As pointed out by Ivan, this solution is incorrect.
All triangles formed are similar to the original triangle (which means they are still obtuse), so this attempt fails.
This leads to an infinite series that fails no matter how far you look into it.
It seems all solutions lie with the absolute midpoint-center of the triangle, working backwards to identify angles which produce solutions where all three angles are < 90° (essentially, variants of equilateral triangles where some of the triangles share one of its vertices at the midpoint-center, as shown in Zandra's solution).
I guess I saw this problem in a Ted-Ed riddle. Here is the link: https://www.youtube.com/watch?v=4peuImhJj44&lc=Ugz-Cgu99VvPnYQfgzt4AaABAg
1 Thing is quite clear that triangle is obtuse triangle so after cutting every angle will be less than 90 and we can make infinite triangle of it
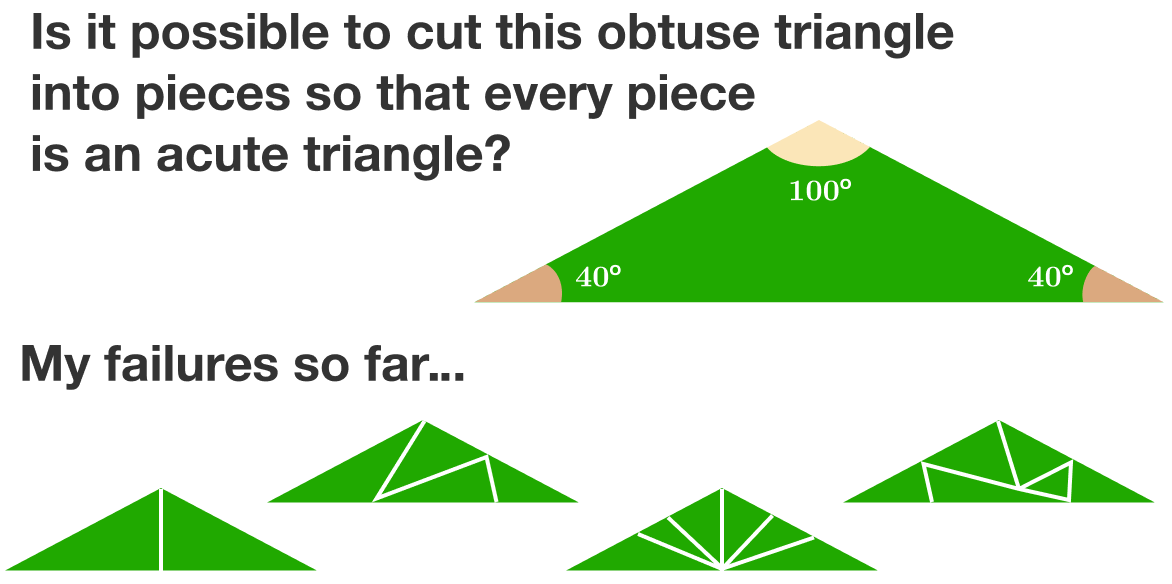
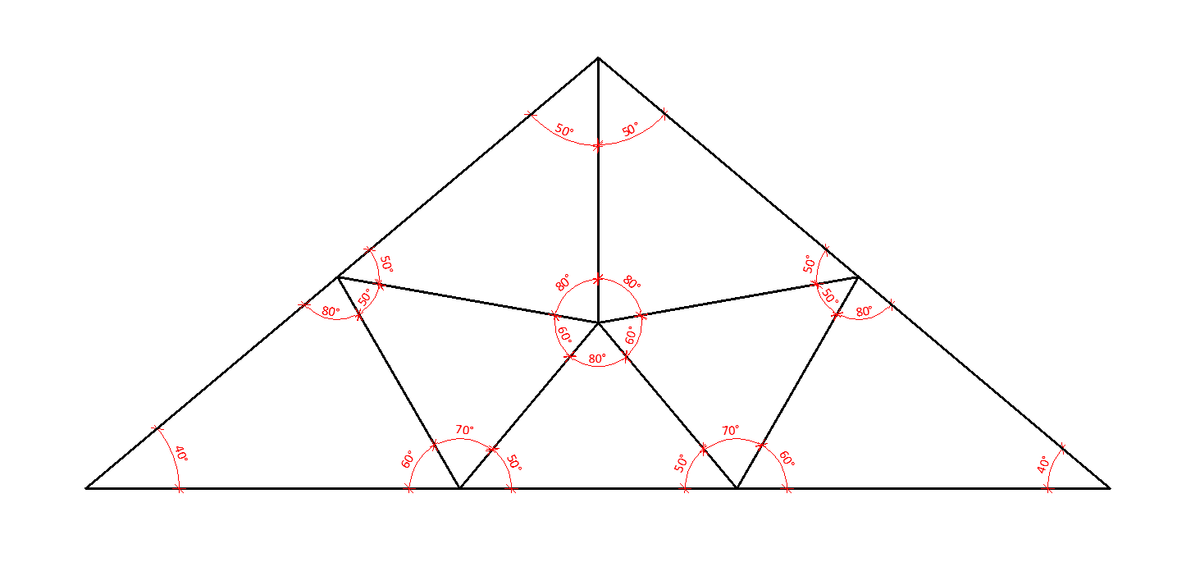
And it's impossible to do it in fewer than 7 pieces!