A geometry problem by คลุง แจ็ค

The formula for distance between two points is $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ This can easily be proven by constructing a right triangle where the line between the points is the hypotenuse and using the Pythagorean theorem.

This is what we get if we want to find the distance between $(x,y)$ and $(0,4)$ : $d=\sqrt{x^2+(4-y)^2}$ And this is what we get if we want to find the distance between $(x,y)$ and $(3,0)$ : $d=\sqrt{(3-x)^2+y^2}$ Adding these together gives us the expression in the question.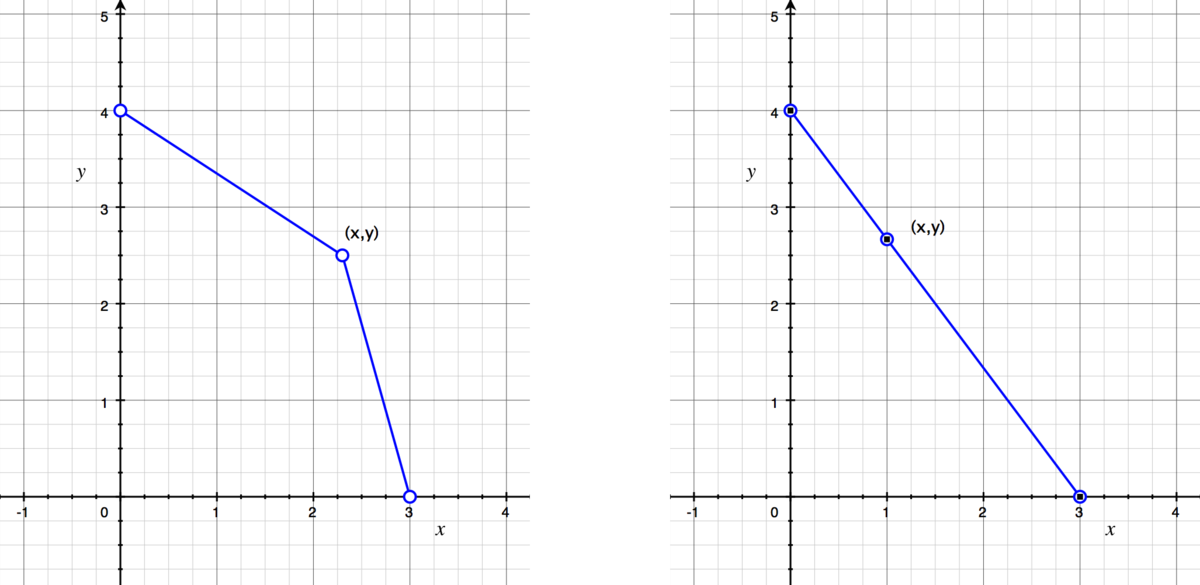 Intuitively, the sum of the distances between the two points must be smallest if $(x,y)$ lies exactly between the two points. In this case, the total distance would just be equal to the distance from $(0,4)$ to $(3,0)$ . $\begin{aligned}d&=\sqrt{4^2+3^2}\\&=5\end{aligned}$ So the minimum value of the expression must be 5.