Take the Centre of Mass, I Dare You!
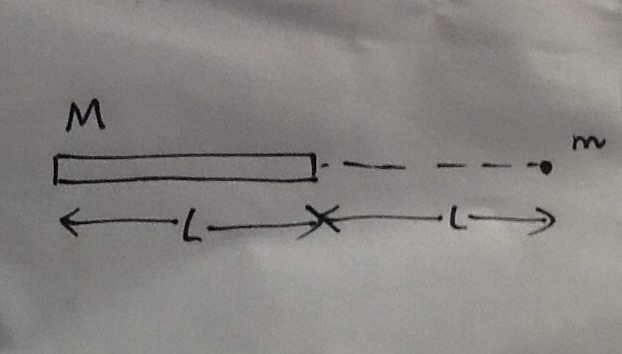 Consider a homogenous rod of length
and mass
, and a point-sized object of mass
, kept at a distance
from one end of the rod, as shown in the figure.
Consider a homogenous rod of length
and mass
, and a point-sized object of mass
, kept at a distance
from one end of the rod, as shown in the figure.
Let the magnitude of force of gravitational attraction be
If , where are coprime, natural numbers, find
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In this problem, taking centre of mass of the rod and finding its attraction with the point is wrong. This method will yield
F = 9 L 2 4 G M m , thus a + b = 1 3 .
This method is incorrect as the force distribution for each point on the rod is different, and non-contradictory.
Thus, let us use calculus to solve this problem.
Consider a small part of the rod of length d x , with mass d M , and let this small part's distance from the point-mass be x
Thus, d F = x 2 G ( d M ) m . However, we cannot integrate this, as the variables do not match. Thus, we must find d M in terms of d x , or x in terms of M .
Let us do the former option, as it would eliminate the variable.
Now, consider linear density λ . Since the rod is homogenous, and the small part of the rod has the same linear density, we get
λ = d x d M = L M , which means that d M = L M d x
Plugging into the force equation, we get d F = ( L G M m ) x 2 1 d x
Now, the limits of this integration must be from L to 2 L , as the minimum distance of any point on the rod from the point mass is L , and the maximum distance is 2 L
Thus, integrating, we get F = ∫ L 2 L ( L G M m ) ( x 2 1 ) d x = L G M m [ x 2 − 1 ] L 2 L = L − G M m [ 2 L 1 − L 1 ] = 2 L 2 G M m
Thus, a = 1 , b = 2 and a + b = 3