Taking it to the next level
In triangle, find the sum of the total number of triangles(excluding degenerate triangles) and quadrilaterals(excluding degenerate quadrilaterals) in the given figure.
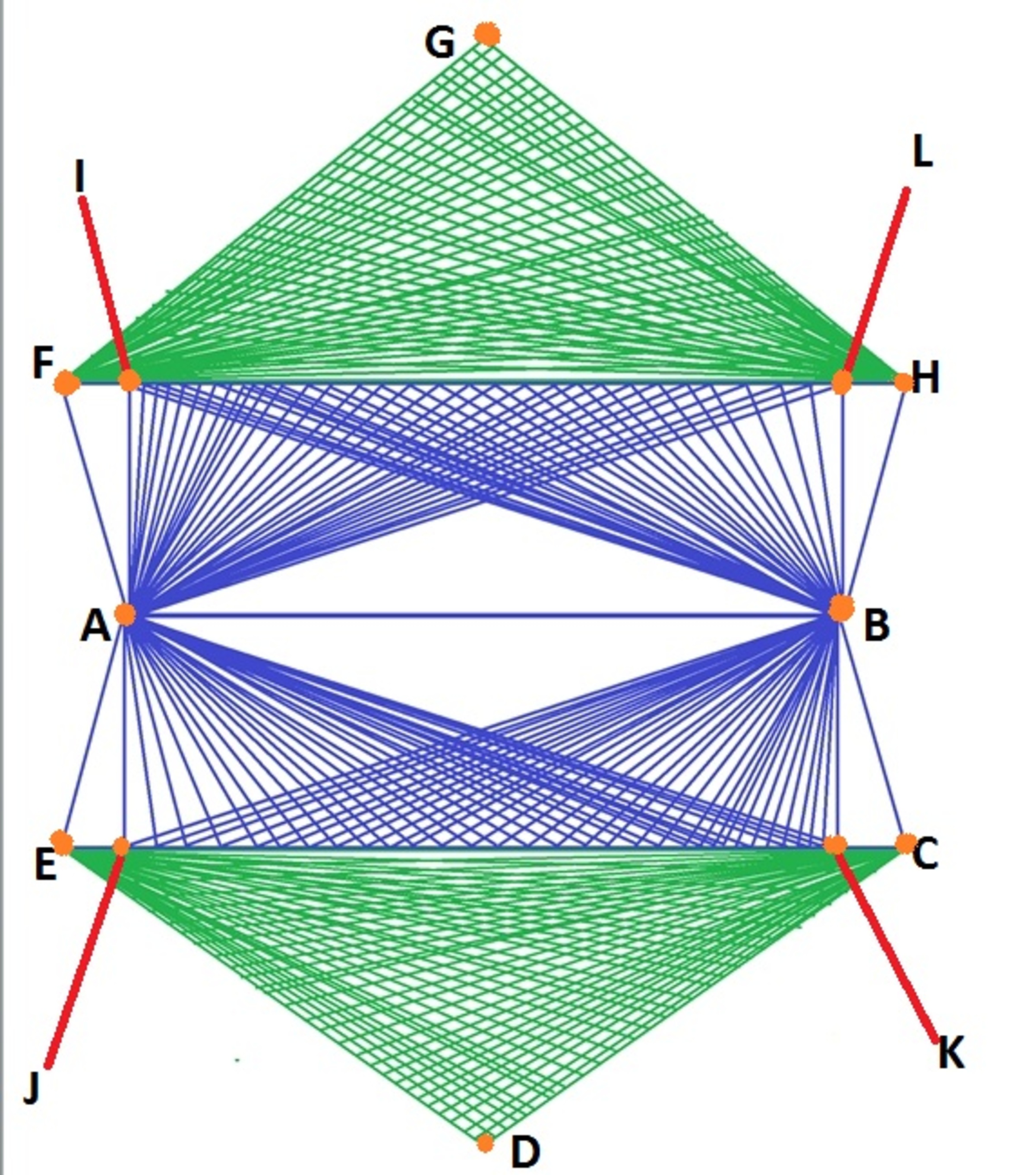
Note : and are perpendicular to .
Line segment FH is parallel to AB.
G is a point on the other side of FILH compared to AB
There are 30 additional points on the line segment IL, which are connected to both A and B with line segments.
There are 27 additional points on the line segment FG, which are connected to H with line segments
There are 27 additional points on the line segment GH, which are connected to F with the line segments.
Line segment EC is parallel to AB.
D is a point on the other side of EJKC compared to AB
There are 30 additional points on the line segment EC, which are connected to both A and B with line segments.
There are 27 additional points on the line segment ED, which are connected to C with line segments
There are 27 additional points on the line segment CD, which are connected to E with line segments.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The total number of t r i a n g l e s = [ ( 1 2 7 8 5 ∗ 2 ) + 6 ] + [ 2 ∗ 1 1 2 8 6 ] = 2 5 5 7 6 + 2 2 5 7 2 = 4 8 1 4 8 .
The total number of q u a d r i l a t e r a l s = 3 0 + [ ( 2 9 + 2 8 + 2 7 + 2 6 + 2 5 + 2 4 + 2 3 + 2 2 + 2 1 + 2 0 + 1 9 + 1 8 + 1 7 + 1 6 + 1 5 + 1 4 + 1 3 + 1 2 + 1 1 + 1 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 ) − 1 ] + 3 + [ 2 9 + 2 8 + 2 7 + 2 6 + 2 5 + 2 4 + 2 3 + 2 2 + 2 1 + 2 0 + 1 9 + 1 8 + 1 7 + 1 6 + 1 5 + 1 4 + 1 3 + 1 2 + 1 1 + 1 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 ] + 1 + [ 2 ∗ 4 2 9 4 9 6 7 2 9 4 0 ] + 1 1 0 + [ 2 ∗ 1 3 1 0 4 4 ]
= 3 0 + 4 3 4 + 3 + 4 3 6 + 8 5 8 9 9 3 4 5 8 8 0 + 1 6 3 4 5 6 2 1 9 + 1 1 0 + 2 6 2 0 8 8
= 8 6 0 6 3 0 6 5 2 0 0
Therefore, the total number of t r i a n g l e s and q u a d r i l a t e r a l s
= 8 6 0 6 3 0 6 5 2 0 0 + 4 8 1 4 8
= 8 6 0 6 3 1 1 3 3 4 8