Taking the Middle
Geometry
Level
2
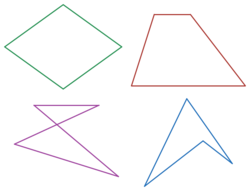What figure do you get when you connect up the midpoints of consecutive sides of a quadrilateral?
Rectangle
None of the rest
Rhombus
Parallelogram
Kite
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
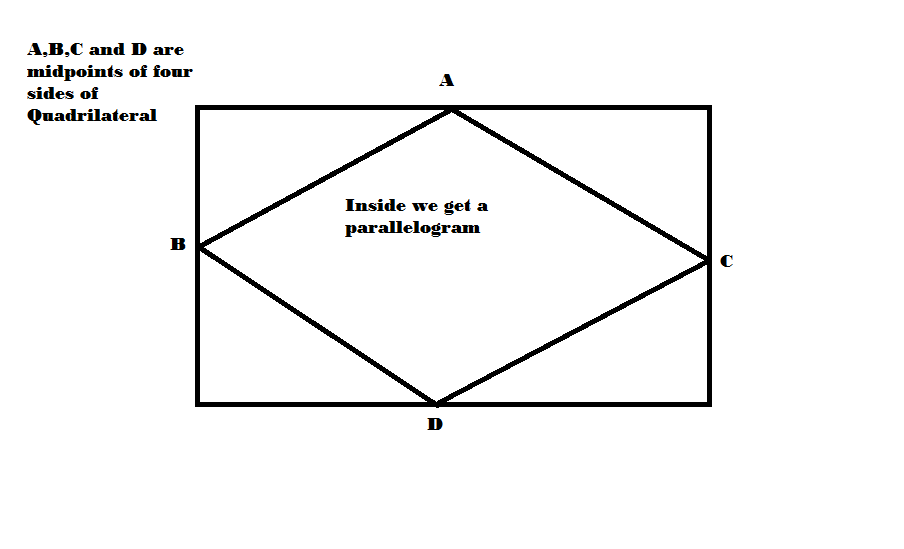
By the Midpoint Theorem we know that joining the midpoints of two consecutive sides will form a line segment that is parallel to and half the length of a diagonal of the original quadrilateral. As there are only two diagonals, the figure created by joining the (consecutive) midpoints of the original quadrilateral will have two pairs of parallel sides, which implies that the figure is a parallelogram.
(The figure created could be a rectangle or rhombus if the original quadrilateral is itself a parallelogram, but this is not the case in general. Also, note that by "diagonal" I mean the line segment joining two non-consecutive vertices, (clockwise or counterclockwise), of the original quadrilateral.)