Taking the Ratio of the Two Volumes
The glass on the left is full of wine, which is in the shape of a cone.
Sam drinks the wine until its height is halved, as shown on the right.
Now, the glass has only ____ of the wine left.
If the height of the wine is halved, how much wine remains?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Thank you for sharing your solution.
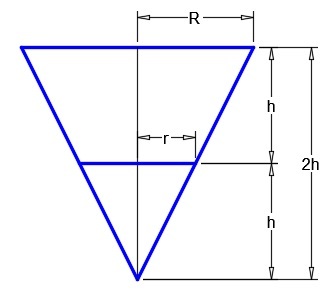 Let
V
1
be the volume of the small cone and
V
2
be the volume of the larger cone. Considering my figure and by similar triangles, we have
Let
V
1
be the volume of the small cone and
V
2
be the volume of the larger cone. Considering my figure and by similar triangles, we have
2 h R = h r ⟹ R = 2 r
The ratio of their volume is
V 2 V 1 = 3 1 π ( R 2 ) ( 2 h ) 3 1 π r 2 h = 2 R 2 r 2
However, R = 2 r . So
V 2 V 1 = 2 ( 2 r ) 2 r 2 = 8 r 2 r 2 = 8 1 ⟹ V 1 = 8 1 V 2
Thank you for sharing your solution.
For solids of similar shade, the volume V is directly proportional to x 3 , where x is a linear dimension of space (one of x , y or z ). In equations:
V V ( x ) ∝ x 3 = k x 3 where k is a constant.
⟹ V ( 2 x ) = k ( 2 x ) 3 = 8 k x 3 = 8 1 V ( x )
Thank you for sharing your solution.
Height is halved, radius is halved
V =πr2/3
So eighth part of the initial
If two similar solids have a scale factor of b a , then corresponding volumes have a ratio of b 3 a 3 . Since the height of the liquid in the second glass is half of the height of the liquid in the first glass, then the scale factor is 2 1 , and the volumes have a ratio of 2 3 1 3 = 8 1 .
Another way to look at it is that since the liquid in the second glass has half the height, it would also have 2 1 the radius for the circle, which translates to 4 1 the area for the circle, which means that the volume ( V = 3 1 A h ) of the liquid in the second glass is 4 1 of 2 1 of the volume of the liquid in the first glass, or 8 1 .