Tangents And Gradients

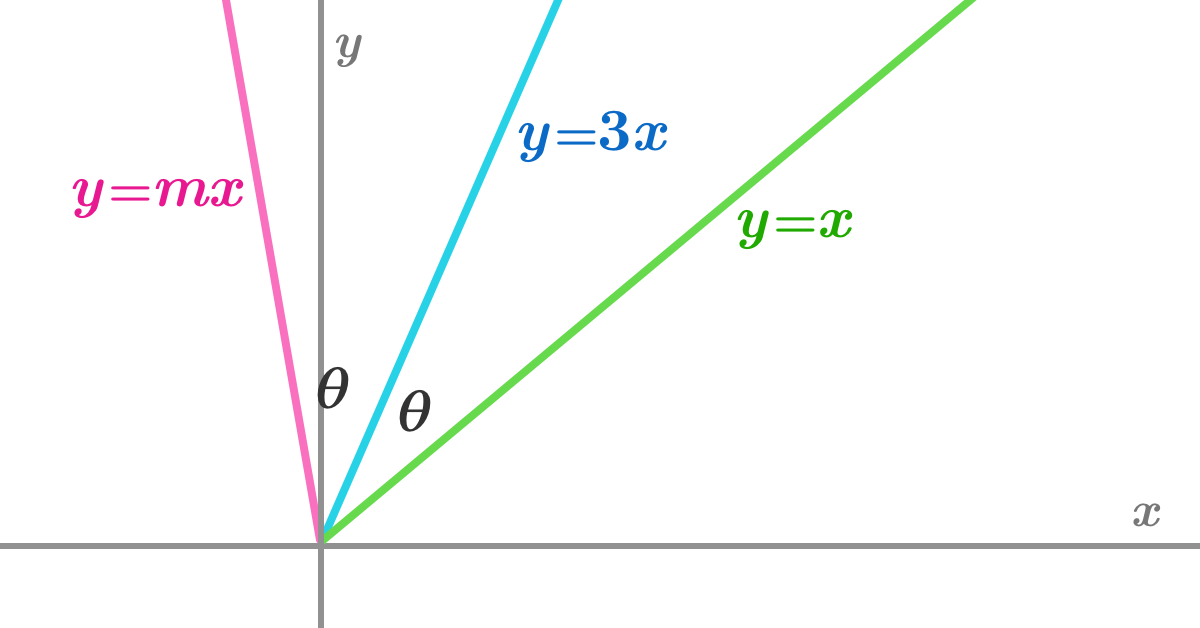
Relevant wiki: Sum and Difference Trigonometric Formulas - Problem Solving

More details :

Let $\theta$ denote the acute angle between the straight lines $y = x$ and $y=3x$ . Since $y =3x$ is an angle bisector of the straight lines $y = mx$ and $y = x$ , then the acute angle between the lines $y=mx$ and $y = 3x$ is also $\theta$ , as shown in the picture above.

Since the tangent function represents the ratio of the rise and the run of the slope a straight line, then $y = x = 1x$ has a gradient of $1 = \tan \dfrac\pi4$ . In other words, the angle formed between the $x$ -axis and the line $y = x$ is $\dfrac\pi4$ (or $45^\circ$ ).

Likewise, the angle between the $x$ -axis and the line $y = 3x$ (of slope 3) is $\theta + \dfrac\pi4$ . So, $\tan \left( \theta + \dfrac\pi4 \right) = 3$ . By applying the compound angle formula for the tangent function , the previous equation can be rewritten as $\dfrac{\tan \theta + \tan \frac\pi4}{1 - \tan \theta \tan \frac\pi4 } = 3$ . Knowing that $\tan \dfrac\pi4 = 1$ , we can simplify the equation to obtain $\tan \theta = \dfrac12$ .

And now we want to find the value of $m$ , where $m = \tan \left( 2\theta + \dfrac\pi4\right)$ . By double angle formula, $\tan 2\theta = \dfrac{2\tan\theta}{1 - \tan^2\theta} = \dfrac43$ . Hence, $m =\boxed{-7}$ .

If y= 3x is angle bisector to both y=x and y=MX then perpendicular distance from any point say (x1;y2) will be same ,just eqate both distance we will find quadratic equation in m ,find m value that will be your solution .