Tangencies
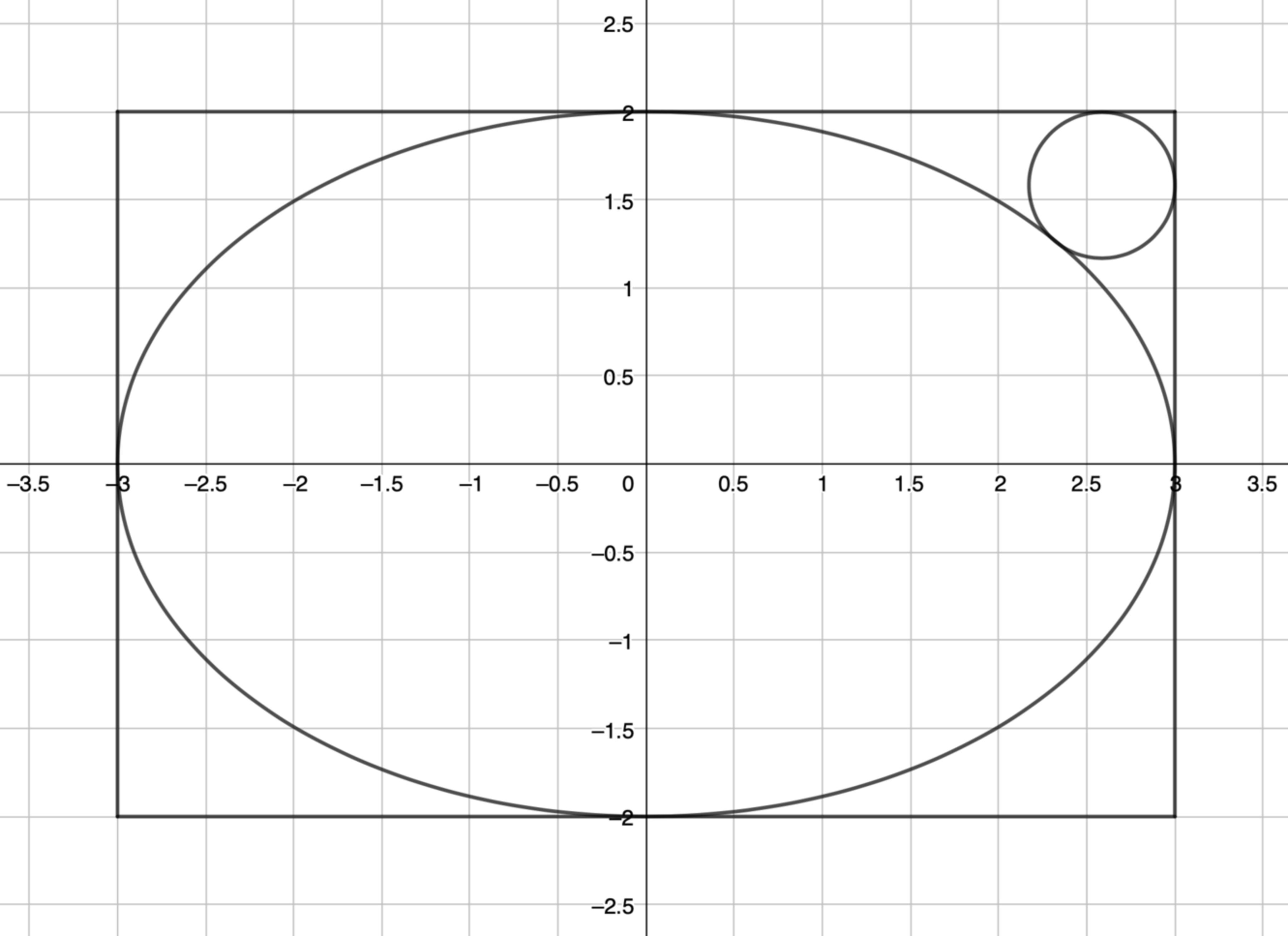
A rectangle inscribes an ellipse of equation 9 x 2 + 4 y 2 = 1 and a circle such that the ellipse and circle are tangent to each other and to the sides of the rectangle as shown.
If the radius of the circle can be expressed as a + b − c − d , where a , b , c , and d are positive integers, submit a + b + c + d .
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thank goodness for Luck! Actually, that is exactly how I approached it except I cheated and asked Wolfram to solve it for me.
I'm crying for hours right now because I can only solve this by summoning Mathematica at the very end.
Here's my miserable anticlimatic solution:
Since we can place the circle in any of the 4 corners of the rectangle, and we can shift the entire graph, Let's consider the following configuration:
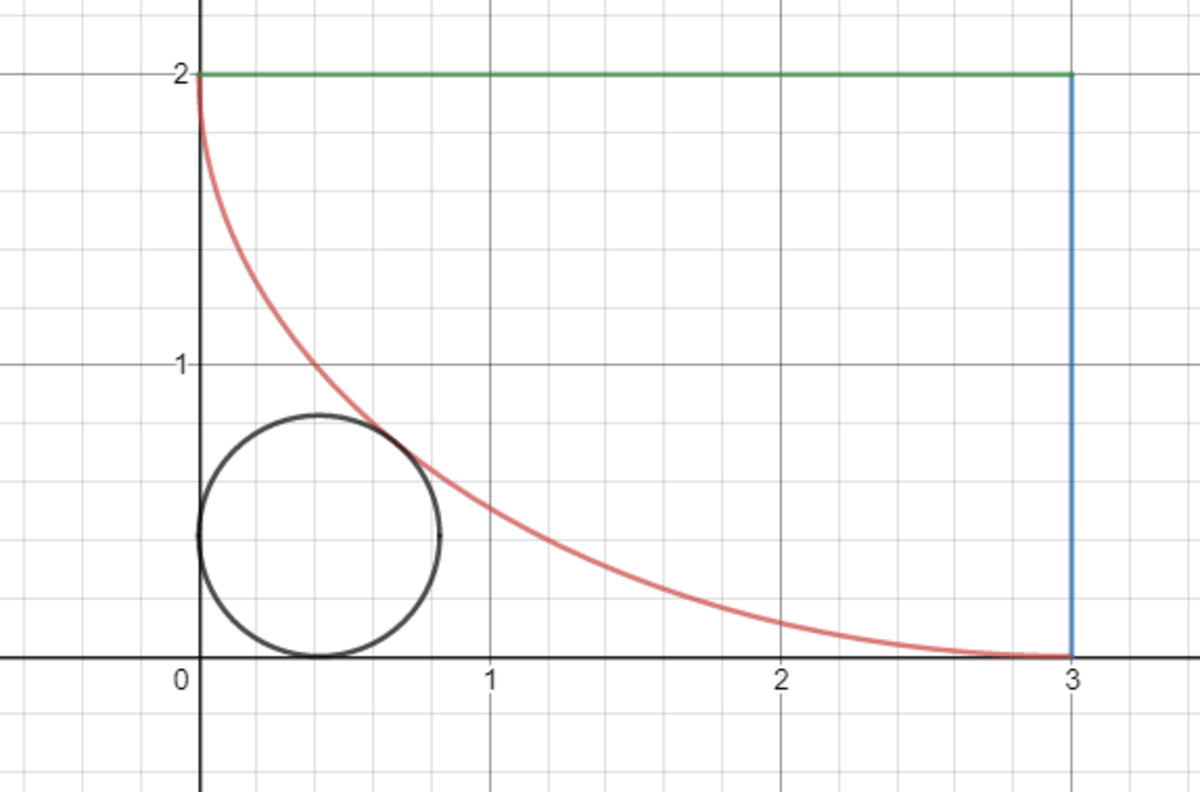
Where the equation of the new (red) quarter ellipse is 9 ( x − 3 ) 2 + 4 ( y − 2 ) 2 = 1 and the equation of the (black) circle is ( x − r ) 2 + ( y − r ) 2 = r 2 . We want to solve for 0 < r < 2 such that these two curves only have one intersection point.
Using the same idea from Chew-Seong to get the gradients at the intersection point, we have d x d y = − 9 4 ⋅ y − 2 x − 3 = − y − r x − r ⟹ r = 4 x − 9 y + 6 − 5 x y + 1 8 x − 1 2 y . Substitute this expression of r into the equation of the ellipse, then expand and simplify to get 1 6 x 4 − 3 2 x 3 y − 9 6 x 3 + 7 2 x 2 y 2 + 4 8 x 2 y + 1 4 4 x 2 − 1 6 2 x y 3 + 4 3 2 x y 2 − 5 0 4 x y + 8 1 y 4 − 3 2 4 y 3 + 3 2 4 y 2 = 0 Now we are left to solve two equations of two variables each. Life is too short for me to solve these equations by hand... So, let me summon the almighty
Mathematica:

Assuming an arbitrary alignment of planets, astrology tells us that the intersection point of ( x , y ) = ( 5 1 5 − 3 1 5 , 5 1 0 − 2 1 0 ) . And hence, r = 5 + 6 − 1 0 − 1 5 .
Log in to reply
Here's another miserable anticlimatic solution:
Using the same configuration from my picture above.
Let the x -coordinate of the intersection point be t , then substituting into the equation of the red ellipse, we have the y -coordinate of the intersection point to be 2 − 3 2 9 − ( t − 3 ) 2 .
And since the center of the black circle is ( r , r ) , then the distance between this center and the intersection point ( t , 2 − 3 2 9 − ( t − 3 ) 2 ) must be r as well.
By Pythagoras' theorem, we have r 2 = ( t − r ) 2 + ( 2 − 3 2 9 − ( t − 3 ) 2 − r ) 2 .
Also, we previously also know that r = 4 x − 9 y + 6 − 5 x y + 1 8 x − 1 2 y , substitute the x and y coordinates as written above. Then we got an equation with a single variable t .
Now let's summon
Mathematicaagain because I'm clearly inadequate here:
If r is the radius of the corner circle, then its center is
C = ( 3 − r , 2 − r )
Let t be the eccentric angle of the ellipse, so that points on the ellipse can be parameterized as
P = ( 3 cos t , 2 sin t )
Two conditions must hold for the point of tangency P :
- The normal vector at P has the same slope as P C .
- P C has a length of r .
Since the normal vector at P is along ( 2 cos t , 3 sin t ) , the first requirement translates into,
2 cos t 3 sin t = ( 3 − r ) − 3 cos t ( 2 − r ) − 2 sin t
which, after re-arranging, becomes,
3 sin t ( ( 3 − r ) − 3 cos t ) − 2 cos t ( ( 2 − r ) − 2 sin t ) = 0
so that,
f 1 = − 2 ( 2 − r ) cos t + 3 ( 3 − r ) sin t − 5 sin t cos t = 0
And the second requirement, becomes,
f 2 = ( ( 3 − r ) − 3 cos t ) 2 + ( ( 2 − r ) − 2 sin t ) 2 − r 2 = 0
This is a nonlinear system of two equations in two unknowns, f ( x ) = 0
It can be readily solved using Newton-Raphson's method (multivariate). My implementation converged in 3 iterations
to r = 0 . 4 1 4 2 2 8 7 3 6 4 0 7 3 8 2 and t = 0 . 6 8 4 7 1 9 2 0 3 0 0 2 2 8 1
Next thing, using a trial-and-error loop, I found that r = 5 + 6 − 1 0 − 1 5
Hence, the answer is 5 + 6 + 1 0 + 1 5 = 3 6
Nice work!
I've checked other cases, and it seems that for the ellipse a 2 x 2 + b 2 y 2 = 1 , the radius of the circle is given by a + b + a b − a ( a + b ) − b ( a + b ) .
Let the radius of the circle be r . Then the equation of the circle is ( x − 3 + r ) 2 + ( y − 2 + r ) 2 = r 2 . Consider the point of contact P ( u , v ) between the circle and the ellipse. Other than satisfying the equations of the ellipse and circle, the gradients of both the ellipse and circle are equal. Therefore
⎩ ⎪ ⎨ ⎪ ⎧ 2 ⋅ 9 x + 2 ⋅ 4 y ⋅ d x d y = 0 2 ( x − 3 + r ) + 2 ( y − 2 + r ) d x d y = 0 ⟹ d x d y = − 9 y 4 x ⟹ d x d y = − y − 2 + r x − 3 + r ⟹ 9 y 4 x = y − 2 + r x − 3 + r
Now P ( u , v ) satisfies the following system of equations
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 9 x 2 + 4 y 2 ( x − 3 + r ) 2 + ( y − 2 + r ) 2 y − 2 + r x − 3 + r = 1 = r 2 = 9 y 4 x . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
Since there are three equations and three unknowns, we can solve the system of equations. What I did was, using equation ( 1 ) , first expressed y in term of x as y = 4 ( 1 − 9 x 2 ) . Using the corresponding values of x and y calculated the value of r using equation ( 3 ) as r = 4 x − 9 y 5 x y + 8 x − 2 7 y . Then went to find the corresponding values of x , y , and r that satisfied equation ( 2 ) . I did this with an Excel spreadsheet with manual iterations. Perhaps @Pi Han Goh can come up with an algebraic solution. I have neither the skills nor the patience.
As if struck by good luck, else I would have to fail @Fletcher Mattox this time, it was found that u 2 = 5 . 6 and v 2 = 1 . 6 or u = 3 5 3 and v = 2 5 2 . Substituting the values into
r = 4 u − 9 v 5 u v + 8 u − 2 7 v = 5 + 6 − 1 0 − 1 5
Therefore a + b + c + d = 5 + 6 + 1 0 + 1 5 = 3 6 .